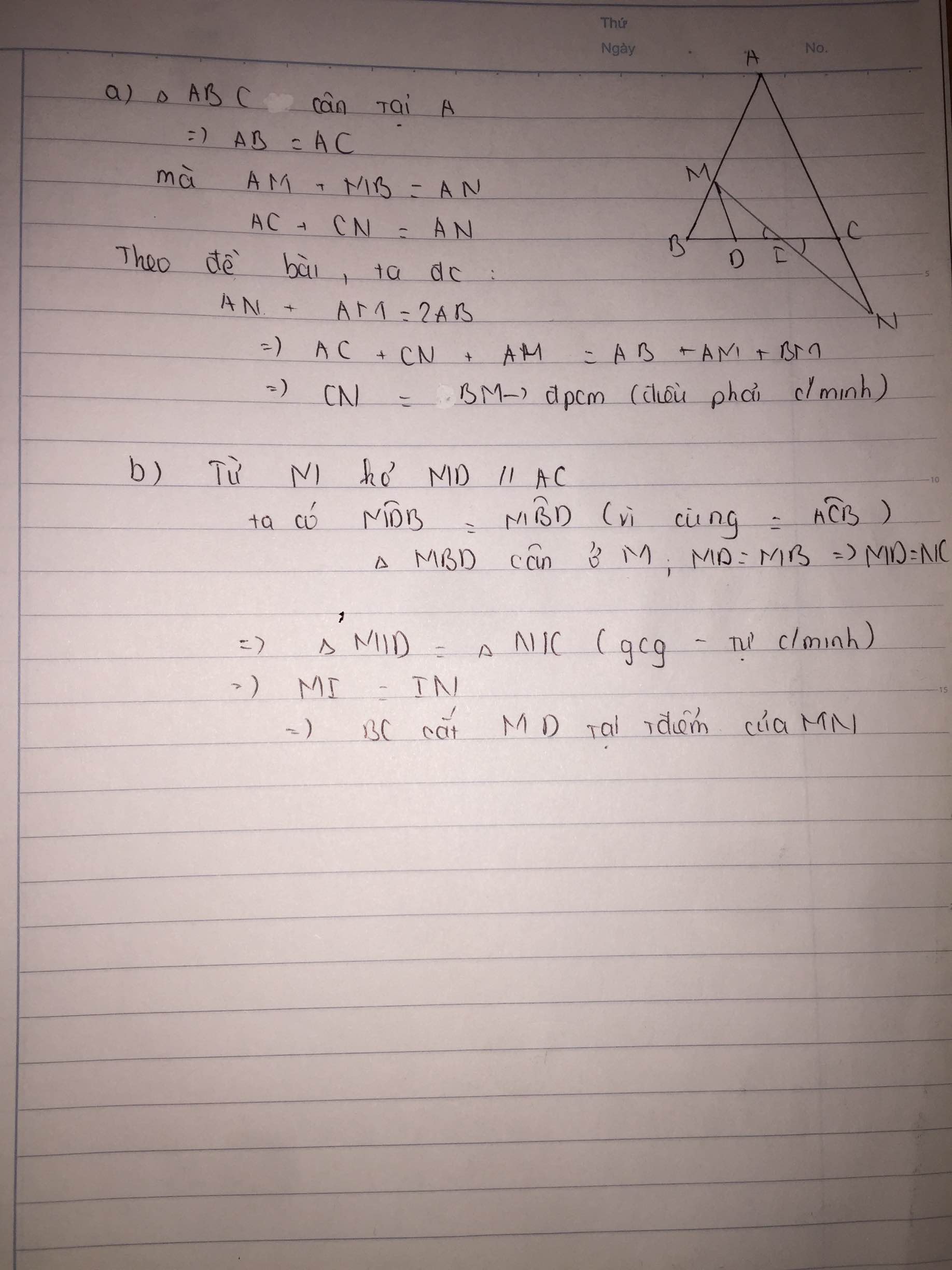Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A M B C N
Trong \(\Delta ABC\)có: \(AB=AC\) (gt)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(2 góc đáy)
Mà \(\widehat{ABC}+\widehat{ABM}=180^o\)
\(\widehat{ACB}+\widehat{ACN}=180^o\)
Nên \(\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\)và \(\Delta ACN\)có:
\(AB=AC\)(gt)
\(\widehat{ABM}=\widehat{ACN}\)(chứng minh trên)
\(MB=NC\)(gt)
Do đó \(\Delta ABM=\Delta ACN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\)

a.2ab=am+an
=> 2ab=am+ac+cn
=> ....=am+ab+cn
=> ab=am+cn
=> am+bn=am+cn
=> bm = cn
b. BC cắt MN tại I
vẽ NE // BC ( e thuộc ab kéo dài )
suy ra gốc aABC = gốc AEN
gốc AEN = góc ABC
mà góc ABC = góc ACB ( ABC cân tại A)
hình thang BCNE là hình thang cân
=> CN = BE
mà CN = BM ( câu a )
=> Bm = BE
BI // NE
BI là đường trung bình MNE=> MI=IN
k mk nhá tks bn
a.2ab=am+an
=> 2ab=am+ac+cn
=> ....=am+ab+cn
=> ab=am+cn
=> am+bn=am+cn
=> bm = cn
b. BC cắt MN tại I
vẽ NE // BC ( e thuộc ab kéo dài )
suy ra gốc aABC = gốc AEN
gốc AEN = góc ABC
mà góc ABC = góc ACB ( ABC cân tại A)
hình thang BCNE là hình thang cân
=> CN = BE
mà CN = BM ( câu a )
=> Bm = BE
BI // NE
BI là đường trung bình MNE=> MI=IN