Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ \(CG\perp EF\), \(BN\perp EF\)( \(G,N\in EF\))
Xét tam giác BMN vuông tại N và tam giác CMG vuông tại G có;
BM = CM( M là trung điểm của BC)
\(\widehat{BMN}=\widehat{CMG}\)(đối đỉnh)
=> \(\Delta BMN=\Delta CMG\)(cạnh huyền - góc nhọn)
=> BN = CG.
Gọi P là giao của đường phân giác góc BAC và EF.
Tam giác AEF có AP vừa là đường phân giác, vừa là đường cao => Tam giác AEF cân tại A.
=> \(\widehat{AEF}=\widehat{AFE}\)mà \(\widehat{AEF}=\widehat{BEN}\)(đối đỉnh) => \(\widehat{BEN}=\widehat{AFE}\).
=> \(90^0-\widehat{BEN}=90^0-\widehat{AFE}\)=> \(\widehat{GCF}=\widehat{NBE}\)
Xét tam giác GCF vuông tại G và tam giác NBE vuông tại N có:
BN = CG( chứng minh trên)
\(\widehat{GCF}=\widehat{NBE}\)(chứng minh trên)
=> \(\Delta GCF=\Delta NBE\)(cạnh góc vuông - góc nhọn kề) => BE = CF(đpcm)

a, \(BH\perp AD\left(gt\right)\Rightarrow\widehat{BHA}=\widehat{BHD}=90^0\)
\(CK\perp AD\left(gt\right)\Rightarrow\widehat{AKC}=90^0\)
Xét \(\Delta BHD\)và \(\Delta CKD\) có:
\(\widehat{BHD}=\widehat{CKD}=90^0\)
\(\widehat{BDH}=\widehat{CDK}\) (đối đỉnh)
Do đó: \(\Delta BHD\infty\Delta CKD\left(g.g\right)\)
b, Xét \(\Delta ABH\) và \(\Delta ACK\) có:
\(\widehat{BAH}=\widehat{CAK}\) (vì AD là tia p/g của góc BAC)
\(\widehat{AHB}=\widehat{AKC}=90^0\)
Do đó: \(\Delta ABH\infty\Delta ACK\left(g.g\right)\)
Suy ra: \(\frac{AB}{AH}=\frac{AC}{AK}\) hay \(AB.AK=AC.AH\)
C, \(\Delta ABH\infty\Delta ACK\left(cmt\right)\Rightarrow\frac{BH}{CK}=\frac{AB}{AC}\left(1\right)\)
\(\Delta BHD=\Delta CKD\left(cmt\right)\Rightarrow\frac{DH}{DK}=\frac{BH}{CK}\left(2\right)\)
Từ (1) và (2), ta được: \(\frac{DH}{DK}=\frac{BH}{CK}=\frac{AB}{AC}\)
d, Gọi giao điểm giữa FM và BH là O và giao điểm giữa FM và CK là I.
Bạn chứng minh được tam giác BOF tại O và tam giác CIE vuông tại I
\(\Delta BOM=\Delta CIM\left(ch.gn\right)\Rightarrow BO=CI\)(2 cạnh tương ứng)
\(AD//FM\left(gt\right)\Rightarrow\hept{\begin{cases}\widehat{BAD}=\widehat{F}\\\widehat{DAC}=\widehat{IEC}\end{cases}}\)(đồng vị)
Suy ra: \(\widehat{F}=\widehat{IEC}\)
Mà \(\hept{\begin{cases}\widehat{F}+\widehat{FBO}=90^0\\\widehat{IEC}+\widehat{ICE}=90^0\end{cases}}\)
Nên \(\widehat{FBO}=\widehat{ICE}\)
Chứng minh được \(\Delta FBO=\Delta ECI\left(g.c.g\right)\Rightarrow BF=CE\)(2 cạnh tương ứng)
Chúc bạn học tốt.
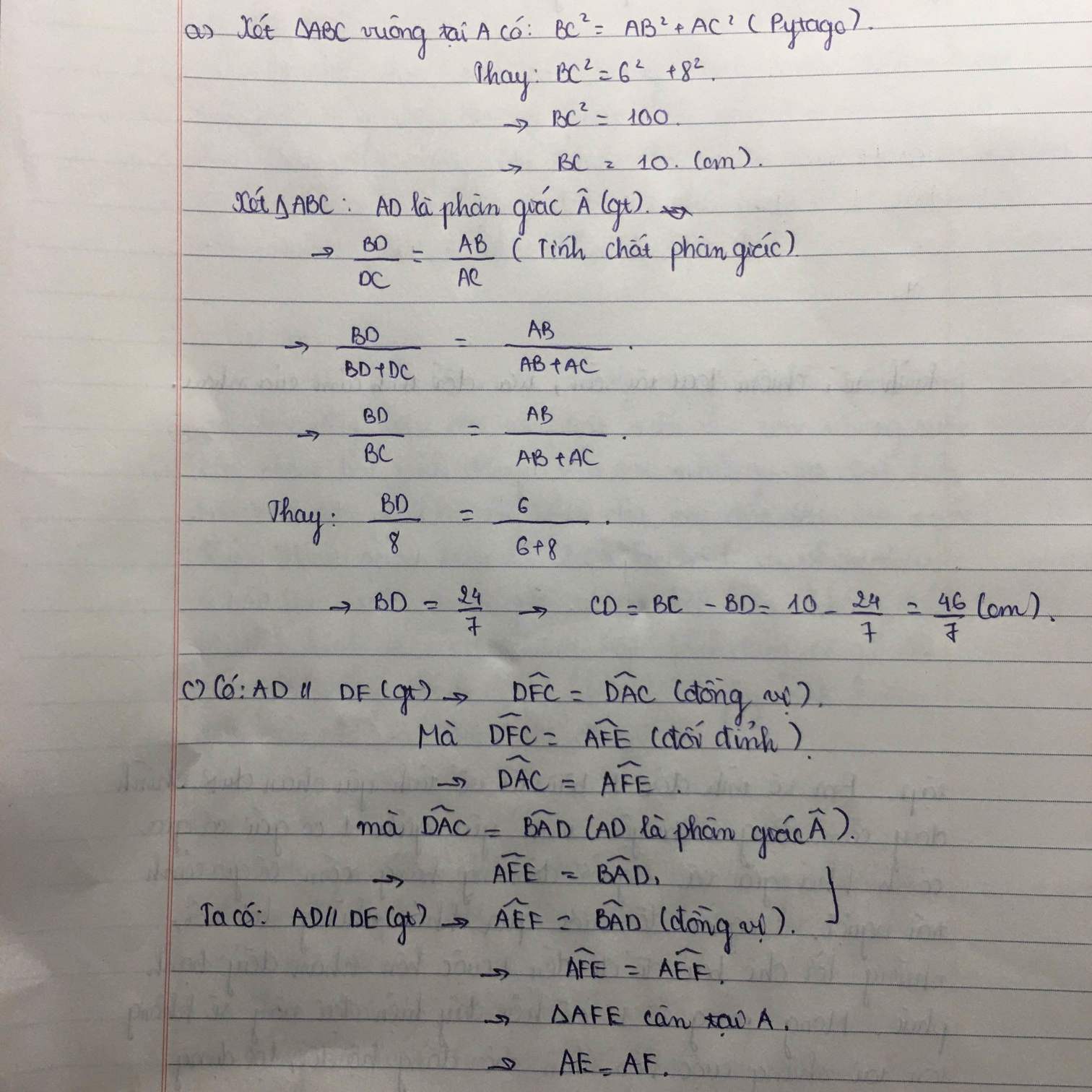
bác cho e xem giải câu này vs