

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





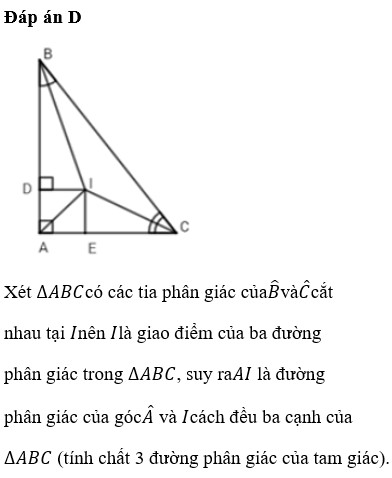
Xét tam giác ABC có các tia phân giác của B ^ và C ^ cắt nhau tại I nên I là giao điểm của ba đường phân giác trong tam giác ABC, suy ra AI là đường phân giác của góc A ^ và I cách đều ba cạnh của tam giác ABC (tính chất 3 đường phân giác của tam giác). Vậy ta loại đáp án A,B và C
Vì I là giao điểm của ba đường phân giác trong tam giác ABC nên => DI = IE(tính chất 3 đường phân giác của tam giác)
Chọn đáp án D

5. ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\) \(a.b=c.d\)
\(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2-2ab}{\left(c+d\right)^2-2cd}\)
Mà a+b = c+ d; ab = cd
=> đfcm
Bài 4:
a: Ta có: I nằm trên đường trung trực của AD
nên IA=ID
Ta có: I nằm trên đường trung trực của BC
nên IB=IC
b: Xét ΔIAB và ΔIDC có
IA=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔIAB=ΔIDC

a, I thuộc đường trung trực của AD (Gt)
=> IA = ID (Đl)
I thuộc đường trung trực của BC (gt)
=> IB = IC (đl)
b, xét ta giác IAB và tam giác IDC có : CD = AB (gt)
IB = IC (câu a)
IA = ID (câu a)
=> tam giác IAB = tam giác IDC (c-c-c)
a) I \(\in\) đường trung trực của BC
\(\Rightarrow IB=IC\)
I \(\in\) đường trung trực của AD
\(\Rightarrow IA=ID\Rightarrow\Delta IAD\) cân \(\Rightarrow\widehat{IAC}=\widehat{IDC}\) ( 1 )
Xét \(\Delta IAB\) và \(\Delta IDC\) có :
\(AB=CD\)
\(IB=IC\)
\(IA=ID\)
\(\Rightarrow\Delta IAB=\Delta IDC\)
\(\Rightarrow\widehat{BAI}=\widehat{CDI}\) ( 2 )
Từ (1) và (2) \(\Rightarrow\widehat{BAI}=\widehat{IAC}\Rightarrow AI\) là phân giác của \(\widehat{BAC}\)