Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi M( x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Biểu diễn hình học của P là đường thẳng và P = 4x + 2y + 3.
Áp dụng bất đẳng thức Bunyakovsky ta có:
P = 4x + 2y + 3 = 4(x – 3) + 2(y – 4) + 23
![]()
Vậy MaxP = 33 

Đáp án B.
Đặt ![]() suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
suy ra tập hợp các điểm M(z) = (x;y) là đường tròn (C) có tâm I(3;4) và bán kính R =
5
Ta có ![]()
![]()
![]()
![]()
![]()
![]()
Ta cần tìm P sao cho đường thẳng ∆ và đường tròn (C) có điểm chung
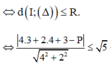
![]()
![]()
Do đó 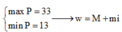
![]()

Đặt \(z=x+yi\)
\(\left|x+yi+x-yi+2\right|+2\left|x+yi-x+yi-2i\right|\le12\)
\(\Leftrightarrow\left|2x+2\right|+4\left|\left(y-1\right)i\right|\le12\)
\(\Leftrightarrow\left|x+1\right|+2\left|y-1\right|\le6\)
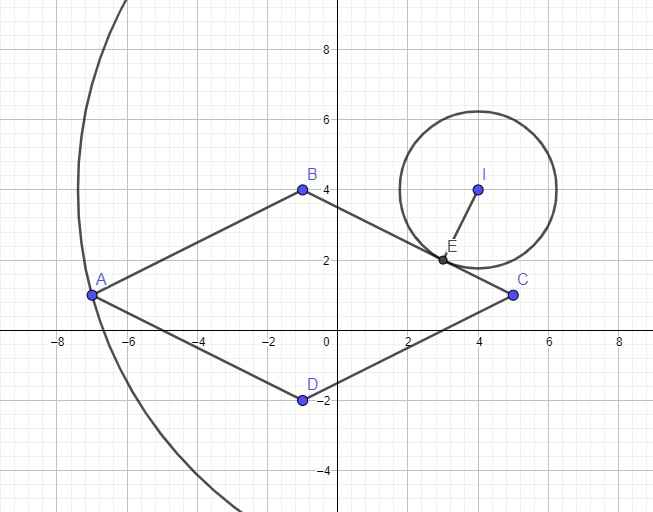
Tập hợp z là miền trong hình thoi (gồm cả biên) với 4 đỉnh: \(A\left(-7;1\right)\) ; \(B\left(-1;4\right)\) ; \(C\left(5;1\right)\) ; \(D\left(-1;-2\right)\)
\(P^2=\left|z-4-4i\right|^2=\left(x-4\right)^2+\left(y-4\right)^2\) có tập hợp là đường tròn (C) tâm \(I\left(4;4\right)\) bán kính \(R=P>0\) sao cho (C) và hình thoi ABCD có ít nhất 1 điểm chung
Từ hình vẽ ta thấy \(P_{max}\) khi (C) đi qua A \(\Rightarrow P=IA\) và \(P_{min}\) khi (C) tiếp xúc BC \(\Rightarrow P=d\left(I;BC\right)\)
\(\overrightarrow{IA}=\left(-11;-3\right)\Rightarrow M=IA=\sqrt{130}\)
\(\overrightarrow{BC}=\left(6;-3\right)\Rightarrow\) đường thẳng BC nhận (1;2) là 1 vtpt
Phương trình BC: \(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)
\(\Rightarrow m=d\left(I;BC\right)=\dfrac{\left|4+2.4-7\right|}{\sqrt{1^2+2^2}}=\sqrt{5}\)
\(\Rightarrow M+m=\sqrt{130}+\sqrt{5}\)

Đáp án C
Phương pháp: Gọi ![]() là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
là số phức cần tìm. Sử dụng giả thiết để đưa ra một hệ điều kiện đẳng thức, bất đẳng thức cho a,b. Sử dụng điều kiện trên để đánh giá và tìm giá trị lớn nhất của P.
Lời giải chi tiết.
Giả sử số phức thỏa mãn yêu cầu bài toán có dạng ![]() Khi đó ta có
Khi đó ta có
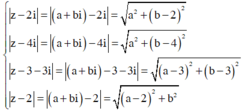
Từ giả thiết ta suy ra
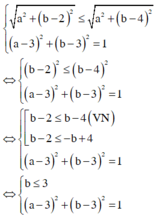
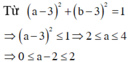
Do đó ![]()
Đẳng thức xảy ra khi và chỉ khi
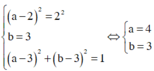
Chú ý. Đối với bài toán liên quan tới cực trị học sinh thường mắc phải sai lầm là quên tìm giá trị để cực trị xảy ra. Điều này có thể dẫn tới việc tìm sai giá trị lớn nhất nhỏ nhất

Giả sử số phức thỏa mãn yêu cầu bài toán có dạng z = a+bi Khi đó ta có
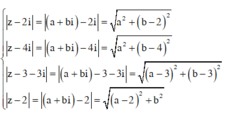
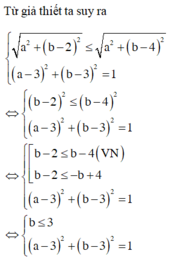
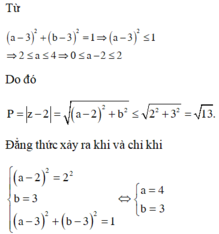
Đáp án C
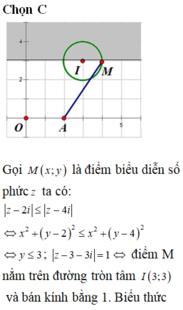

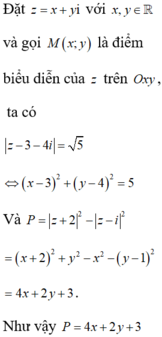
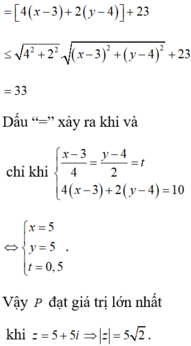

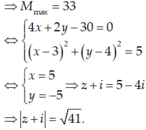
Đặt \(z=x+yi\Rightarrow\) quỹ tích z là các điểm M thuộc đường tròn \(\left(x-2\right)^2+\left(y+3\right)^2=5\) có tâm \(I\left(2;-3\right)\) bán kính \(R=\sqrt{5}\)
\(P=x^2+\left(y+1\right)^2-\left(x-2\right)^2-y^2=4x+2y-3\)
\(P=4\left(x-2\right)+2\left(y+3\right)-1\le\sqrt{\left(4^2+2^2\right)\left[\left(x-2\right)^2+\left(y+3\right)^2\right]}-1=11\)
\(\Rightarrow P_{max}=11\) khi \(\frac{x-2}{4}=\frac{y+3}{2}\Rightarrow x=2y+8\)
Thay vào \(\left(x-2\right)^2+\left(y+3\right)^2=5\) tìm được \(x;y\Rightarrow\) tìm được \(z\)