Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{x-4}{y-3}=\frac{4}{3}\Rightarrow\frac{x-4}{4}=\frac{y-3}{3}\)
Áp dụng TC của DTSBN ta có:
\(\frac{x-4}{4}=\frac{y-3}{3}=\frac{x-4-y+3}{4-3}=\frac{5-1}{1}=4\)
Suy ra: (x-4)/4=4 =>x-4=16=>x=20
(y-3)/3=4=>y-3=12=>x=15
x-4/y-3=4/3
=>3.(x-4)=4.(y-3)
=>3x-12=4y-12
=>3x=4y
Mà x-y=5=>x=y+5
=>3.(y+5)=4y
=>3y+15=4y=>4y-3y=15=>y=15
Khi đó x=15+5=20
Vậy x=20;y=15

ĐK: a khác 1/2
\(P=\frac{1}{2a-1}\sqrt{25a^4\left(1-4a+4a^2\right)}\)
\(=\frac{1}{2a-1}\sqrt{\left(5a^2\right)^2\left(2a-1\right)^2}=\frac{5a^2}{2a-1}\left|2a-1\right|\)
Với 2a-1>0 <=> a>1/2
\(P=5a^2\)
Với 2a-a<0 <=> a<1/2
\(P=-5a^2\)


vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

\(M>\frac{x}{x+y+z+t}+\frac{y}{x+y+z+t}+\frac{z}{x+y+z+t}+\frac{t}{x+y+z+t}=\frac{x+y+z+t}{x+y+z+t}=1\)
Mà \(\frac{a}{b}<1\) thì \(\frac{a}{b}<\frac{a+m}{b+m}\) ; \(m\in N\)*
Do đó \(M<\frac{x+t}{x+y+z+t}+\frac{y+z}{x+y+z+t}+\frac{z+x}{x+y+z+t}+\frac{t+y}{x+y+z+t}=\frac{2\left(x+y+z+t\right)}{x+y+z+t}=2\)
Vậy 1 < M < 2 nên M không phải là số tự nhiên/

\(\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}+...+\frac{1}{100^2}>\frac{1}{5.6}+\frac{1}{6.7}+\frac{1}{7.8}+...+\frac{1}{100.101}\)
\(=\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+...+\frac{1}{100}-\frac{1}{101}=\frac{1}{5}-\frac{1}{101}=\frac{96}{505}>\frac{1}{6}\)
\(\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}+...+\frac{1}{100^2}<\frac{1}{4.5}+\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{99.100}\)
\(=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{99}-\frac{1}{100}=\frac{1}{4}-\frac{1}{100}<\frac{1}{4}\)
Suy ra: điều cần chứng minh
đặt 1/5^2+1/6^2+,,,+1/100^2=A
*chứng minh A<1/4
ta có: \(\frac{1}{5^2}=\frac{1}{5.5}<\frac{1}{4.5}\)
\(\frac{1}{6^2}=\frac{1}{6.6}<\frac{1}{5.6}\)
...
\(\frac{1}{100^2}=\frac{1}{100.100}<\frac{1}{99.100}\)
\(=>A<\frac{1}{4.5}+\frac{1}{5.6}+...+\frac{1}{99.100}=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+...+\frac{1}{99}-\frac{1}{100}\)
\(=>A<\frac{1}{4}-\frac{1}{100}<\frac{1}{4}=>A<\frac{1}{4}\left(1\right)\)
*chứng minh A>1/6
ta có \(\frac{1}{5^2}=\frac{1}{5.5}>\frac{1}{5.6}\)
\(\frac{1}{6^2}=\frac{1}{6.6}>\frac{1}{6.7}\)
...
\(\frac{1}{100^2}=\frac{1}{100.100}>\frac{1}{100.101}\)
\(=>A>\frac{1}{5.6}+\frac{1}{6.7}+...+\frac{1}{100.101}=\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{100}-\frac{1}{101}\)
\(=>A>\frac{1}{5}-\frac{1}{101}>\frac{1}{6}=>A>\frac{1}{6}\) (2)
từ (1) và (2)=>1/6<A<1/4 hay 1/6<1/5^2+...+1/100^2<1/4(đpcm)
tick nhé
 bit lm bài này k giup tui
bit lm bài này k giup tui
Đáp án A
Cho số phức z = x + yi (x,y ∈ R) , S(x,y) là điểm biểu diễn của z trên hệ trục tọa độ Oxy
Lấy các điểm A(2; - 3), B( - 2; - 1)
Phương trình
=> Tập hợp các điểm S là đường elip (E) có tiêu điểm A(2; - 3), B( - 2; - 1) và có độ dài trục lớn là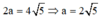
Lấy M(4; - 4). Dễ dàng kiểm tra được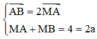
Suy ra, M là một đỉnh và nằm trên trục lớn của elip (E).
Gọi I là trung điểm AB => I(0; - 2), N là điểm đối xứng của M qua I. Khi đó, với mọi điểm