Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đặt w = x + yi , x ; y ∈ ℝ . Số phức w được biểu diễn bởi điểm M(x;y).
Ta có:
w = 3 + 4 i z + i = x + yi
⇔ z = x + y − 1 i 3 + 4 i = x + y − 1 i 3 − 4 i 25 = 3 x + 4 y − 4 + − 4 x + 3 y − 3 i 25
⇒ z = 1 25 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 4
⇔ 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 100 2
⇔ 3 x + 4 y 2 + − 4 x + 3 y 2 − 8 3 x + 4 y + 16 − 6 − 4 x + 3 y + 9 = 10000
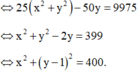
Vậy số phức w được biểu diễn bởi đường tròn tâm I(0;1), bán kính R = 20 và có phương trình: x 2 + y − 1 2 = 400 .

Đáp án D
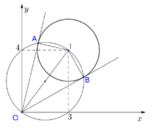
Gọi các tiếp điểm là A và B. Khi đó tọa độ A, B được xác định là giao điểm của đường tròn (C) và đường tròn đường kính OI.
Phương trình đường tròn đường kính OI (tâm , bán kính bằng 5 2 ):
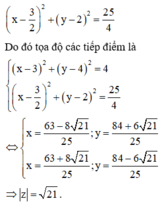

Đáp án C
Cách 1: Số phức z được biểu diễn bởi điểm M(x;y).
Số phức z 1 được biểu diễn bởi điểm A(1;-1).
Em có: z − 1 + i = 2 ⇒ MA = 2 .
Vậy tập hợp điểm M là đường tròn tâm A(1;-1), bán kính R = 2 và có phương trình: x − 1 2 + y + 1 2 = 4 .
Cách 2: Đặt z = x + yi , x ; y ∈ ℝ . Số phức z được biểu diễn bởi điểm M(x;y).
Em có:
z − 1 + i = 2 ⇔ x − 1 + y + 1 i = 2 ⇔ x − 1 2 + y + 1 2 = 2 ⇔ x − 1 2 + y + 1 2 = 4
Vậy tập hợp điểm M là đường tròn tâm I(1;-1), bán kính R = 2 và có phương trình:
x − 1 2 + y + 1 2 = 4 .

Đáp án D
Gọi các tiếp điểm là A và B. Khi đó tọa độ A, B được xác định là giao điểm của đường tròn (C) và đường tròn đường kính OI.


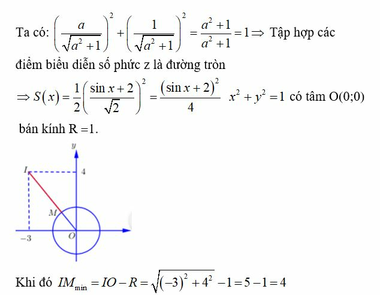




Đáp án D
Ta có 3 - 4 i z - 4 z = 8 ⇔ 3 - 4 i z = 8 + 4 z ( * )
Lấy môđun hai vế của (*) và sử dụng công thức z 1 z 2 = z 1 . z 2 , ta được
* ⇔ 3 - 4 i z = 8 + 4 z ⇔ 3 - 4 i . z = 4 2 + 1 z ⇔ 5 z = 4 2 + 1 z
⇔ 5 z 2 = 4 2 z + 1 ⇔ 5 z 2 - 8 z - 4 = 0 ⇔ z = 2
Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó O M = x 2 + y 2 = z = 2 ∈ 1 2 ; 9 4 .