Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:

Trên mp tọa độ \(Oxy\) ta xét các điểm \(A(-2,1);B(4,7);C(1,-1)\). Tập hợp các điểm biểu diễn số phức $z$ là $M$
Theo bài ra ta có:
\(|z-(-2+i)|+|z-(4+7i)|=6\sqrt{2}\Leftrightarrow MA+MB=6\sqrt{2}\)
Mà \(AB=\sqrt{(-2-4)^2+(1-7)^2}=6\sqrt{2}\Rightarrow MA+MB=AB\)
Do đó điểm \(M\) nằm trên đoạn thẳng $AB$
Đề bài yêu cầu tìm max min của \(|z-(1-i)|\), tức là tìm max, min của đoạn \(MC\)
Dựa vào hình vẽ, suy ra \(MC_{\min}=d(C,AB)\).
Do biết tọa độ $A,B$ nên dễ dàng viết được PTĐT $AB$ là : \(y=x+3\)
\(\Rightarrow MC_{\min}=d(C,AB)=\frac{|1-(-1)+3|}{\sqrt{2}}=\frac{5\sqrt{2}}{2}\)
Vì \(M\) chỉ chạy trên đoạn $AB$ nên \(MC_{\max}=CA\) hoặc $CB$
Thấy \(CA< CB\Rightarrow CM_{\max}=CB=\sqrt{(4-1)^2+(7+1)^2}=\sqrt{73}\) khi \(M\equiv B\)
Vậy \(\left\{\begin{matrix} |z-1+i|_{\min}=\frac{5\sqrt{2}}{2}\\ |z-i+1|=\sqrt{73}\end{matrix}\right.\)

a) (3 + 2i)z – (4 + 7i) = 2 – 5i
⇔(3+2i)z=6+2i
<=> z = \(\dfrac{\text{6 + 2 i}}{\text{3 + 2 i}}\) = \(\dfrac{22}{13}\) - \(\dfrac{6}{13}\)i
b) (7 – 3i)z + (2 + 3i) = (5 – 4i)z
⇔(7−3i−5+4i)=−2−3i
⇔z= \(\dfrac{\text{− 2 − 3 i}}{\text{2 + i}}\) = \(\dfrac{-7}{5}\) - \(\dfrac{4}{5}i\)
c) z2 – 2z + 13 = 0
⇔ (z – 1)2 = -12 ⇔ z = 1 ± 2 √3 i
d) z4 – z2 – 6 = 0
⇔ (z2 – 3)(z2 + 2) = 0
⇔ z ∈ { √3, - √3, √2i, - √2i}

Xét riêng: \(\frac{\left|z\right|^4}{z^2}=\left(\frac{\left|z\right|^2}{z}\right)^2=\left(\left|z\right|^2\cdot\frac{\overline{z}}{\left|z\right|^2}\right)=\left(\overline{z}\right)^2=w\)
Thay w vào phương trình, ta có:
\(w^2+w+\frac{200}{1-7i}=0\\ \Delta=1-4\cdot\frac{200}{1-7i}=-15-112i\\ \Rightarrow\Delta=\left(7-8i\right)^2\)
Phương trình có 2 nghiệm là:
\(\left[\begin{matrix}w=-4+4i\\w=3-4i\end{matrix}\right.\Leftrightarrow\left[\begin{matrix}z=-4-4i\\z=3+4i\end{matrix}\right.\)
Xin lỗi, dòng đầu viết nhầm. Phải là "đặt \(w=\overline{z}\)" mới đúng.

a) (3 + 4i)z = (2 + 5i) – (1 – 3i) = 1 + 8i
Vậy z=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45iz=1+8i3+4i=(1+8i)(3−4i)25=3525+2025i=75+45i
b) (4 + 7i)z – (5 – 2i) = 6iz ⇔ (4 + 7i)z – 6iz = 5 – 2i
⇔ (4 + i)z = 5 – 2i
⇔z=5−2i4+i=(5−2i)(4−i)17⇔z=1817−1317i
Tìm \(\overline{z}\) biết :
a) \(z=1-i\sqrt{2}\)
b) \(z=-\sqrt{2}+i\sqrt{3}\)
c) \(z=5\)
d) \(z=7i\)

a) (3 - 5i) + (2 + 4i) = (3 + 2) + (-5i + 4i) = 5 - i.
b) (-2 - 3i) + (-1 - 7i) = (-2 - 1) + (-3i - 7i) = -3 - 10i
c) (4 + 3i) - (5 - 7i) = (4 - 5) + (3i + 7i) = -1 + 10i
d) (2 - 3i) - ( 5 - 4i) = (2 - 5) + (-3i + 4i) = -3 + i
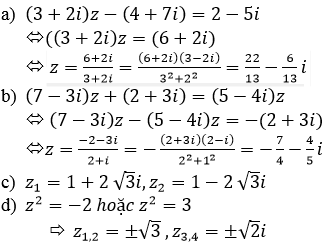
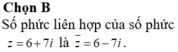
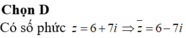
Đáp án D