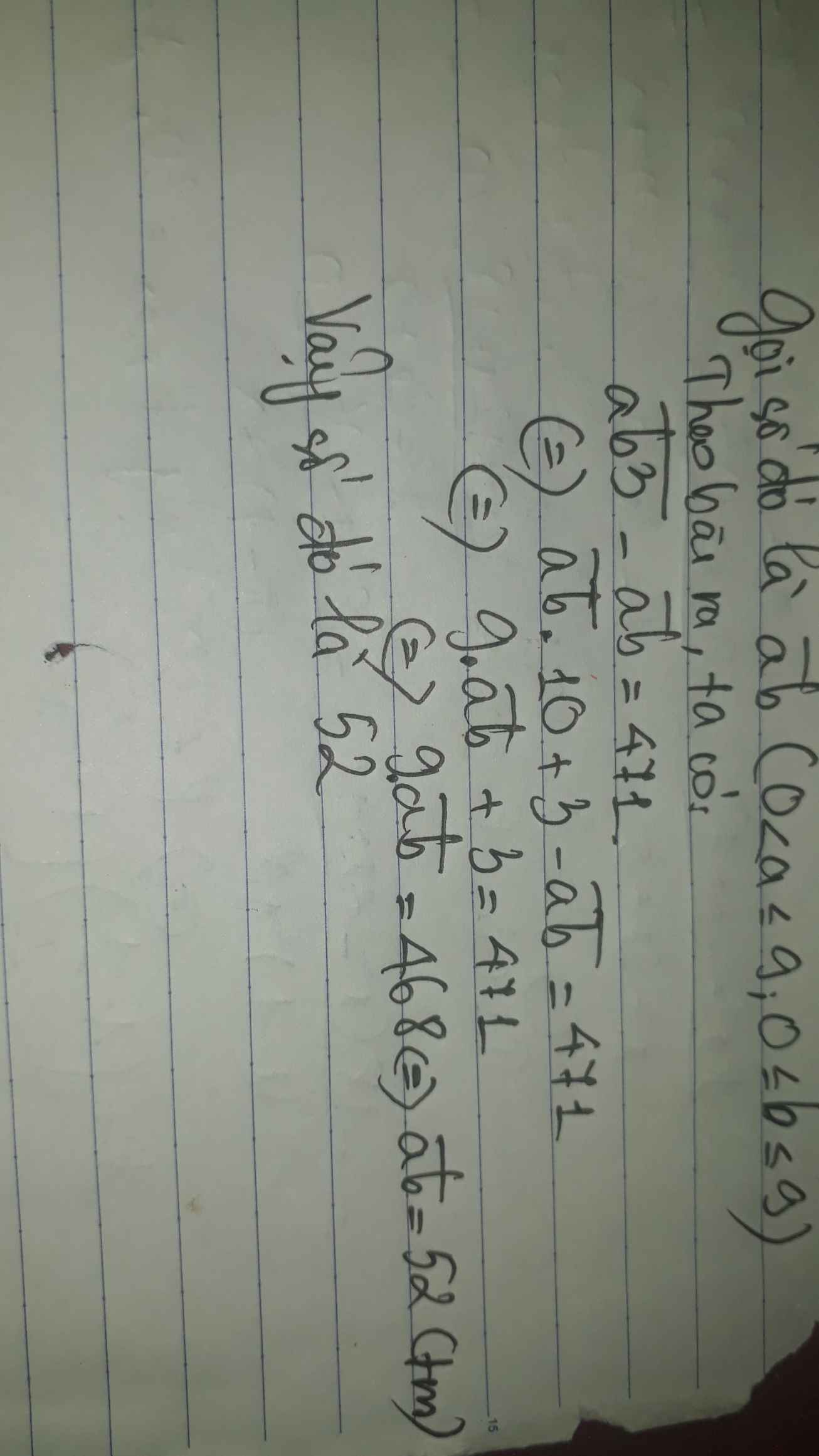Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện: $a,b$ là số tự nhiên; $a,b\leq 9; a\neq 0$
Theo bài ra ta có:
$\overline{ab3}-\overline{ab}=471$
$\overline{ab}\times 10+3-\overline{ab}=471$
$\overline{ab}\times (10-1)+3=471$
$\overline{ab}\times 9+3=471$
$\overline{ab}\times 9=468$
$\overline{ab}=468:9=52$
Vậy số cần tìm là $52$

đặt số cần tìm là abc
ta có abc0 = abc + 3555
abc x 10 = abc + 3555
abc x 9 = 3555
abc = 395
gọi số cần tìm là : abc
Nếu thêm chữ số 0 vào bên phải số đó thì số đó sẽ gấp lên 10 lần . Vậy
abc = 3555 : ( 10 - 1 ) = 395
Vậy số cần tìm là 395

Câu hỏi của Châu Uyên Ly - Toán lớp 6 - Học toán với OnlineMath
Bạn tham khảo nhé!

c - a = 5 có nghĩa là hiệu hai chữ số c và a là 5: ta có 6 - 1 = 5
vậy ta có 6 và 1 trong đó c = 6 và a = 1.
thay vào abc ta được 1b6. Hỏi nếu viết số đó theo thứ tự ngược lại thì được số mới hơn số đã cho bao nhiêu đơn vị? thì ta viết được 6b1
ta lấy 6b1 - 1b6 = 495
đáp án 495.