Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải: Biết chữ số hàng trăm, hàng chục, hàng đơn vị là 3 số tự nhiên liên tiếp tăng dần nên các số đó là: 123, 234,345,456,567,789. Và khi viết theo thứ tự ngược lại thì các số đó là: 321,432,543,654,765,987.
Số đó sẽ tăng lên là: 321 - 123 = 198
432 - 234 = 198
Tương tự như thế
.......................
Đáp số: 198

gọi số cần tìm là a7 ta có
a7-a=295
a*10+7-a=295
a*10-a+7=295
9a+7=295
9a=295-7
9a=288
a=288:9
a=32
vậy số cần tìm là 327

Chọn B.

Xét hai bộ (1;2;6) và (3;4;5) thì ta lập được 3!.3!= 36 số, trong đó các chữ số 1,2,6 có mặt ở hàng trăm
Nghìn 36 : 3 =12 lần, hàng chục nghìn 12 lần, hàng nghìn 12 lần và các chữ số 3,4,5 cũng có mặt ở hàng trăm, chục, đơn vị 12 lần.
Tổng các số trong trường hợp này là:
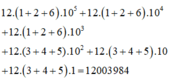
Tương tự ở hai cặp còn lại ta cũng có tổng các số bằng 12003984.
Khi đó tổng các phần tử của M là 12003984.3 = 36011952

Gọi số tự nhiên có 4 chữ số khác nhau đôi một được chọn từ các chữ số 0; 1; 2; 3;4;5;6 là a b c d .
a có 6 cách chọn; các số còn lại có A 6 3 cách chọn. Suy ra số phần tử của S là 6 . A 6 3 = 720
Do đó n Ω = 720
Gọi A là biến cố: “số được chọn là số chẵn đồng thời chữ số hàng đơn vị bằng tổng các chữ số hàng chục, trăm và nghìn”.
Số được chọn thỏa mãn yêu cầu đề bài nếu
d ∈ 0 ; 2 ; 4 ; 6 d = a + b + c ⇒ d ∈ 4 ; 6 d = a + b + c .
* Trường hợp 1: Số có dạng a b c 4 với a + b + c = 4 suy ra tập { a;b;c } là { 0;1;3 }. Vì a,b,c đôi một khác nhau nên có 2 cách chọn a; 2 cách chọn b; 1 cách chọn c. Do đó số các số thuộc dạng này là 2 . 2 . 1 = 4
* Trường hợp 2: Số có dạng a b c 6 với a + b + c = 6 suy ra tập { a;b;c } có thể là một trong các tập { 0;1;5 }; { 0;2;4 }; { 1;2;3 }
+ Nếu { a;b;c } là tập { 0;1;5 } hoặc { 0;2;4 } thì mỗi trường hợp có 4 số (tương tự trường hợp trên)
+ Nếu { a;b;c } là tập { 1;2;3 } thì có P 3 = 3! = 6 số.
Do đó số các số thuộc dạng này là 4 + 4 + 6 = 14
Qua hai trường hợp trên, ta suy ra n(A): = 14 + 4 = 18.
Vậy xác suất cần tìm là
P A = n A n Ω = 18 720 = 1 40
Đáp án C

Đáp án D.
Số cần lập có dạng:
a b ¯ a ; b ∈ 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 ; a < b .
Với mỗi cách chọn 2 số từ các số đã cho ta được một số thõa mãn yêu cầu bài toán.
Do đó có C 9 2 = 36 số.

Ta có 1188 +ab= abcd(đặt tính theo cột dọc nha).
Nếu ờ hàg chục là phép cộg k nhớ thì ab = 11, suy ra cd là 99.
Số 1199. Nếu ở hàg chục là phép cộg có nhớ thì ab = 12, suy ra cd là 00. Số 1200
