Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tam giác SAB đều \(\Rightarrow SH\perp AB\)
Mà \(\left\{{}\begin{matrix}AB=\left(SAB\right)\cap\left(ABCD\right)\\\left(SAB\right)\perp\left(ABCD\right)\end{matrix}\right.\) \(\Rightarrow SH\perp\left(ABCD\right)\)
Gọi N là trung điểm SC \(\Rightarrow MN\) là đường trung bình tam giác SCD
\(\Rightarrow\left\{{}\begin{matrix}MN||CD\\MN=\dfrac{1}{2}CD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}MN||AH\\MN=AH\end{matrix}\right.\) \(\Rightarrow AMNH\) là hbh
\(\Rightarrow AM||HN\Rightarrow AM||\left(SHC\right)\)
\(\Rightarrow d\left(AM;SC\right)=d\left(AM;\left(SHC\right)\right)=d\left(A;\left(SHC\right)\right)\)
Mặt khác H là trung điểm AB \(\Rightarrow d\left(A;\left(SHC\right)\right)=d\left(B;\left(SHC\right)\right)\)
Từ B kẻ \(BE\perp HC\Rightarrow BE\perp\left(SHC\right)\) (do \(SH\perp BE\))
\(\Rightarrow BE=d\left(B;\left(SHC\right)\right)\)
Hệ thức lượng: \(BE=\dfrac{BH.BC}{CH}=\dfrac{BH.BC}{\sqrt{BH^2+BC^2}}=\dfrac{a\sqrt{5}}{5}\)
b.
Từ D kẻ \(DF\perp HC\Rightarrow DF\perp\left(SHC\right)\) (do \(SH\perp DF\))
\(\Rightarrow DF=d\left(D;\left(SHC\right)\right)\)
\(DF=DC.cos\widehat{FDC}=DC.cos\widehat{BCH}=\dfrac{DC.BC}{CH}=\dfrac{DC.BC}{\sqrt{BC^2+BH^2}}=\dfrac{2a\sqrt{5}}{5}\)

a.
Do tam giác SAB đều \(\Rightarrow SB=AB=a\)
Trong tam giác SBC ta có:
\(SB^2+BC^2=2a^2=SC^2\)
\(\Rightarrow\Delta SBC\) vuông tại B (pitago đảo)
\(\Rightarrow BC\perp SB\)
Mà \(BC\perp AB\left(gt\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
Do \(SH\in\left(SAB\right)\Rightarrow BC\perp SH\) (1)
Lại có SAB là tam giác đều, mà SH là đường trung tuyến (H là trung điểm AB)
\(\Rightarrow SH\) đồng thời là đường cao hay \(SH\perp AB\) (2)
(1);(2) \(\Rightarrow SH\perp\left(ABCD\right)\)
b.
\(SH\perp\left(ABCD\right)\Rightarrow\) HM là hình chiếu vuông góc của SM lên (ABCD)
\(\Rightarrow\widehat{SMH}\) là góc giữa SM và (ABCD) hay \(\alpha=\widehat{SMH}\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều cạnh a)
\(HM=BC=a\) \(\Rightarrow tan\alpha=\dfrac{SH}{HM}=\dfrac{\sqrt{3}}{2}\)
c.
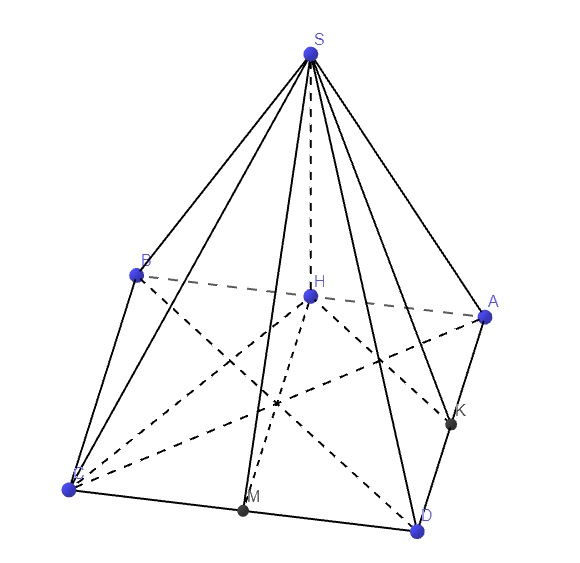
Do H là trung điểm AB, K là trung điểm AD \(\Rightarrow\) HK là đường trung bình tam giác ABD
\(\Rightarrow HK||BD\)
Mà \(BD\perp AC\) (hai đường chéo hình vuông)
\(\Rightarrow HK\perp AC\) (3)
Lại có \(SH\perp\left(ABCD\right)\Rightarrow SH\perp AC\) (4)
(3);(4) \(\Rightarrow AC\perp\left(SHK\right)\Rightarrow AC\perp SK\)

S A B C D H K O M
Trong mp(SAB) từ S dựng dường vuông góc với AB cắt AB tại H
Ta có
\(\left(SAB\right)\perp\left(ABCD\right)\) và AB là giao tuyến của 2 mp
\(SH\perp AB\)
\(\Rightarrow SH\perp\left(ABCD\right)\Rightarrow SH\perp CK\) (1)
Ta có AB=BC=CD=AD=a (gt)
DH cắt CK tại O
Xét tg vuông ADH và tg vuông DCK
AD=CD=a
\(AH=\dfrac{AB}{2}=\dfrac{a}{2}\)
\(DK=\dfrac{AD}{2}=\dfrac{a}{2}\)
=> tg ADK = tg DCK \(\Rightarrow\widehat{AHD}=\widehat{DKC}\)
Mà \(\widehat{ADH}+\widehat{AHD}=90^o\)
\(\Rightarrow\widehat{ADH}+\widehat{DKC}=90^o\)
=> tg DOK vuông tạo O \(\Rightarrow CK\perp DH\) (2)
Từ (1) và (2) \(\Rightarrow CK\perp\left(SDH\right)\)
Trong mp (SDH) từ O dựng đường thẳng vuông góc với SD cắt SD tại M
Ta có \(CK\perp\left(SDH\right);OM\in\left(SDH\right)\Rightarrow CK\perp OM\)
=> OM cùng vuông góc với SD và CK => OM là khoảng cách giữa SD và CK
Do SAB là tg đều => SA=SB=AB=a
Xét tg vuông SAH
\(SH=\sqrt{SA^2-AH^2}=\sqrt{a^2-\dfrac{a^2}{4}}=\dfrac{a\sqrt{3}}{2}\)
Xét tg vuông ADH
\(DH=\sqrt{AD^2+AH^2}=\sqrt{a^2+\dfrac{a^2}{4}}=\dfrac{a\sqrt{5}}{2}\)
Ta có \(SH\perp\left(ABCD\right)\left(cmt\right);DH\in\left(ABCD\right)\Rightarrow SH\perp DH\)
Xét tg vuông SDH
\(SD=\sqrt{SH^2+DH^2}=\sqrt{\dfrac{3a^2}{4}+\dfrac{5a^2}{4}}=a\sqrt{2}\)
Xét tg vuông ODK và tg vuông ADH có chung \(\widehat{ADH}\)
=> tg ODK đồng dạng với tg ADH
\(\Rightarrow\dfrac{DO}{AD}=\dfrac{DK}{DH}\Rightarrow DO=\dfrac{AD.DK}{DH}=\dfrac{a.\dfrac{a}{2}}{\dfrac{a\sqrt{5}}{2}}=\dfrac{a\sqrt{5}}{5}\)
Xét tg vuông ODM và tg vuông SDH có chung \(\widehat{SDH}\)
=> tg ODM đồng dạng với tg SDH
\(\Rightarrow\dfrac{OM}{SH}=\dfrac{DO}{SD}\Rightarrow OM=\dfrac{SH.DO}{SD}=\dfrac{\dfrac{a\sqrt{3}}{2}.\dfrac{a\sqrt{5}}{5}}{a\sqrt{2}}\)
Phần tính toán bạn kiểm tra lại nhé, đại khái cách làm là như thế

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)

Đáp án B.
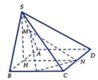
Gọi H là trung điểm của cạnh AB. Khi đó SH ⊥ (ABCD)
Ta có SH ⊥ AB; AB ⊥ HN; HN ⊥ SH và SH = 3
Chọn hệ trục tọa độ Oxyz sao cho H trùng với O, B thuộc tia Ox, N thuộc tia Oy và S thuộc tia Oz. Khi đó: B(1;0;0), A(-1;0;0), N(0;2 3 ;0), C(1;2 3 ;0)
D(-1;2 3 ;0), S(0;0; 3 ), M( - 1 2 ; 0 ; 3 2 ), P(1; 3 ;0)
Mặt phẳng (SCD) nhận
![]()
làm một vectơ pháp tuyến; mặt phẳng (MNP) nhận
![]()
làm một vectơ pháp tuyến.
Gọi φ là góc tạo bởi hai mặt phẳng (MNP) và (SCD) thì
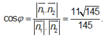
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng
![]()
nhưng lại tính sai ![]() Do đó tính được
Do đó tính được
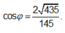
Phương án B: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]()
Do đó tính được
![]()
Phương án C: Sai do HS tính đúng ![]() nhưng lại tính sai
nhưng lại tính sai
![]() Do đó tính được
Do đó tính được 


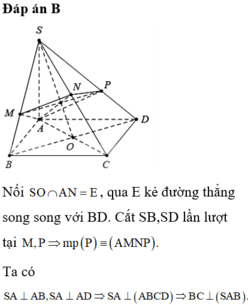

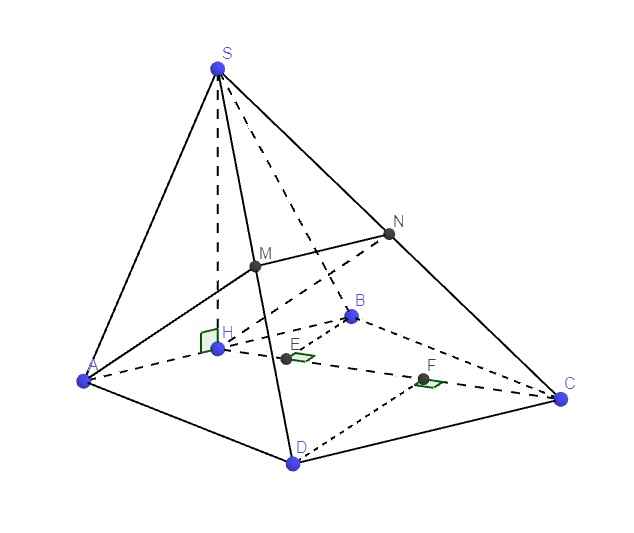
Gọi H là trung điểm AB thì \(SH\perp\left(ABCD\right)\)
Gọi E là trung điểm DH thì NE là đường trung bình trong tam giác SHD nên \(NE||SH\)
Đồng thời ME là đường trung bình trong hình thang BCDH nên \(ME||AB\)
\(\Rightarrow\left(MNE\right)||\left(SAB\right)\)
\(\Rightarrow d\left(AP,MN\right)=d\left(\left(MNE\right);\left(SAB\right)\right)=BM=\dfrac{a}{2}\)