Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. tìm đenta phẩy
sau đó cho đenta phẩy >0
tìm x1+x2,x1*x2 theo hệ thức viets
thay vào ra mà

\(a,\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\forall m\)
Nên pt đã cho luôn có 2 nghiệm phân biệt với mọi m
b, Theo Vi-ét \(\hept{\begin{cases}x_1+x_2=m\\x_1x_2=m-1\end{cases}}\)
Ta có \(B=\frac{2x_1x_2+3}{x_1^2+x_2^2+2\left(1+x_1x_2\right)}=1\)
\(\Leftrightarrow\frac{2x_1x_2+3}{\left(x_1+x_2\right)^2+2}=1\)
\(\Leftrightarrow\frac{2\left(m-1\right)+3}{m^2+2}=1\)
\(\Leftrightarrow\frac{2m+1}{m^2+2}=1\)
\(\Leftrightarrow2m+1=m^2+2\)
\(\Leftrightarrow m^2-2m+1=0\)
\(\Leftrightarrow\left(m-1\right)^2=0\)
\(\Leftrightarrow m=1\)

Bài 1/
a/ Ta có: ∆' = (m - 1)2 + 3 + m
= m2 - m + 4 = \(\frac{15}{4}+\left(x-\frac{1}{2}\right)^2>0\)
Vậy PT luôn có 2 nghiệm phân biệt.
Theo vi et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3-m\end{cases}}\)
Theo đ
Bài 1/
a/ Ta có: ∆' = (m - 1)2 + 3 + m
= m2 - m + 4 = \(\frac{15}{4}+\left(x-\frac{1}{2}\right)^2>0\)
Vậy PT luôn có 2 nghiệm phân biệt.
Theo vi et ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m-1\right)\\x_1x_2=-3-m\end{cases}}\)
Theo đề bài thì
\(x^2_2+x^2_1\ge10\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2\ge10\)
\(\Leftrightarrow\left(2m-2\right)^2-2\left(-3-m\right)\ge0\)
Làm tiếp sẽ ra. Câu còn lại tương tự

dùng phương pháp Vi-ét ko hoàn toàn
(mình đăng lên youtube rồi đấy)
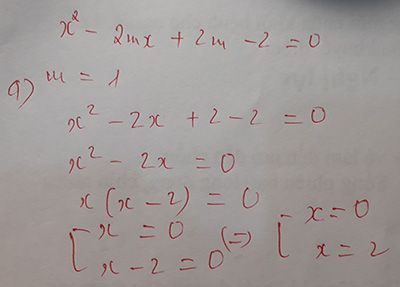
\(\Delta=\left(m-1\right)^2+8>0;\forall m\) nên pt luôn có 2 nghiệm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2\end{matrix}\right.\)
\(\left(1-\dfrac{2}{x_1+1}\right)^2+\left(1-\dfrac{2}{x_2+1}\right)^2=1\)
\(\Leftrightarrow\left(\dfrac{x_1-1}{x_1+1}\right)^2+\left(\dfrac{x_2-1}{x_2+1}\right)^2=1\)
\(\Leftrightarrow\left(\dfrac{x_1-1}{x_1+1}+\dfrac{x_2-1}{x_2+1}\right)^2-2\left(\dfrac{x_1-1}{x_1+1}\right)\left(\dfrac{x_2-1}{x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{\left(x_1-1\right)\left(x_2+1\right)+\left(x_1+1\right)\left(x_2-1\right)}{\left(x_1+1\right)\left(x_2+1\right)}\right)^2-2\left(\dfrac{x_1x_2-\left(x_1+x_2\right)+1}{x_1x_2+x_1+x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{2x_1x_2-2}{x_1x_2+x_1+x_2+1}\right)^2-2\left(\dfrac{x_1x_2-\left(x_1+x_2\right)+1}{x_1x_2+x_1+x_2+1}\right)=1\)
\(\Leftrightarrow\left(\dfrac{-6}{m-2}\right)^2+2\left(\dfrac{m}{m-2}\right)=1\)
\(\Leftrightarrow36\left(\dfrac{1}{m-2}\right)^2+4\left(\dfrac{1}{m-2}\right)+1=0\)
Pt trên vô nghiệm nên ko tồn tại m thỏa mãn yêu cầu
Tới đó đặt \(\dfrac{1}{m-2}=t\) là thành 1 pt bậc 2 bình thường, bấm máy thấy nó vô nghiệm là đủ kết luận rồi em