Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\Delta'=\left[-\left(m+1\right)\right]^2-4m+m^2\)
\(\Delta'=m^2+2m+1+m^2-4m=2m^2-2m+1\)
\(\Delta'=2\left(m-\frac{1}{2}\right)^2+\frac{1}{2}>0\)
=> pt luôn có 2 nghiệm phân biệt
b) Theo hệ thức viet, ta có: \(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=4m-m^2\end{cases}}\)
Theo bài ra, ta có: A = |x1 - x2|
A2 = (x1 - x2)2 = (x1 + x2)2 - 4x1x2
A2 = [2(m + 1)]2 - 4(4m - m2)
A2 = 4m2 + 8m + 4 - 8m + 4m2 = 8m2 + 4 \(\ge\)4 với mọi m
Dấu "=" xảy ra <=> m = 0
Vậy MinA = 4 khi m = 0
a) Xét \(\Delta'=\left(m+1\right)^2-\left(4m-m^2\right)=2m^2-2m+1=m^2+\left(m-1\right)^2>0\)với mọi m
Vậy pt trên luôn có 2 nghiệm phân biệt với mọi m
b) Gọi x1 ; x2 là 2 nghiệm của pt trên . Theo hệ thức Viet , ta có :
\(\hept{\begin{cases}x_1+x_2=2\left(m+1\right)\\x_1x_2=4m-m^2\end{cases}}\)
Xét \(A^2=\left|x_1-x_2\right|^2=\left(x_1+x_2\right)^2-4x_1x_2=4\left(m+1\right)^2-4\left(4m-m^2\right)\)
\(=8m^2-8m+4=2\left(4m^2-4m+1\right)+2=2\left(2m-1\right)^2+2\ge2\)
Dấu " = " xảy ra khi 2m - 1 = 0
Vậy \(A^2\ge2\Leftrightarrow A=\left|x_1-x_2\right|\ge\sqrt{2}\)
Dấu " = " xảy ra khi \(m=\frac{1}{2}\)
Do đó minA \(=\sqrt{2}\)khi \(m=\frac{1}{2}\)

Câu a:
Đặt \(x^2=t\left(t>0\right)\)phương trinh \(x^4+\left(1-m\right)x^2+2m-2=0\left(1\right)\)trở thành \(t^2+\left(1-m\right)t+2m+2=0\left(2\right)\)
Để (1) có 4 nghiệm phân biệt thì phương trình (2) phải có 2 nghiệm phân biệt tức
\(\Delta>0\Leftrightarrow\left(1-m\right)^2-4\left(2m-2\right)>0\)
\(m^2-10m+9>0\Leftrightarrow\left(m-1\right)\left(m-9\right)>0\Leftrightarrow\orbr{\begin{cases}m>9\\m< 1\end{cases}}\)
Câu b:
phương trình (2) có hai nghiệm phân biệt \(t_1,t_2\)tương ứng phương trình (1) có 4 nghiệm phân biệt \(x_1,x_2,x_3,x_4\)thỏa mãn \(\hept{\begin{cases}t_1=-x_1=x_3\\t_2=-x_2=x_4\end{cases}}\)(theo tính chất đối xứng nghiệm của hàm trùng phương bậc 4)
theo viet ta có :\(\hept{\begin{cases}t_1+t_2=1-m\\t_1t_2=2m-2\end{cases}}\)
Xét \(\frac{x_1x_2x_3}{2x_4}+\frac{x_1x_2x_4}{2x_3}+\frac{x_1x_3x_4}{2x_2}+\frac{x_2x_3x_4}{2x_1}=2013\)
\(VT=\frac{\left(x_1x_2x_3\right)^2}{2x_1x_2x_3x_4}+\frac{\left(x_1x_2x_4\right)^2}{2x_1x_2x_3x_4}+\frac{\left(x_1x_3x_4\right)^2}{2x_1x_2x_3x_4}+\frac{\left(x_4x_2x_3\right)^2}{2x_1x_2x_3x_4}\)
\(=\frac{\left(x_1x_2\right)^2\left(x^2_3+x^2_4\right)}{2x_1x_2x_3x_4}+\frac{\left(x_4x_3\right)^2\left(x_1^2+x_2^2\right)}{2x_1x_2x_3x_4}\)
thay biến x bằng biến t ta có
\(VT=\frac{\left(t_1t_2\right)^2\left(t_1^2+t^2_2\right)}{2t_1t_2}+\frac{\left(t_1t_2\right)^2\left(t_1^2+t^2_2\right)}{2t_1t_2}=\frac{2\left(t_1t_2\right)^2\left(t_1^2+t^2_2\right)}{2t_1t_2}\)
\(=\left(t_1t_2\right)\left(t_1^2+t^2_2\right)=\left(t_1^2+t^2_2-2t_1t_2\right)t_1t_2\)
thế m theo viet vào ta có :
\(\left(2m-2\right)\left(\left(1-m\right)^2-2\left(2m-2\right)\right)=2013\)
\(\Leftrightarrow2m^3-8m^2+17m-2023=0\)
Đến đây giải dễ rùi bạn gải nốt tìm m nhé

Bạn ghi lại đề, \(x_1^2-2mx_1+2m-m\) xuất hiện 2 con m ở cuối nên chắc là bạn ghi nhầm chỗ nào đó

có \(\Delta'=\left[-\left(m-1\right)\right]^2-m^2+m+5\)
\(\Delta'=m^2-2m+1-m^2+m+5\)
\(\Delta'=-m+6\)
để pt (1) có 2 nghiệm \(x_1;x_2\) \(\Leftrightarrow-m+6>0\)
\(\Leftrightarrow m< 6\)
theo định lí \(Vi-et\) \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1.x_2=m^2-m-5\end{cases}}\)
theo bài ra \(\frac{x_1}{x_2}+\frac{x_2}{x_1}+\frac{10}{3}=0\)
\(\Leftrightarrow\frac{x_1^2+x_2^2}{x_1.x_2}+\frac{10}{3}=0\) ( \(x_1.x_2\ne0\Leftrightarrow m^2-m-5\ne0\))
\(\Leftrightarrow\frac{\left(x_1+x_2\right)^2-2x_1.x_2}{x_1.x_2}=\frac{-10}{3}\)
\(\Leftrightarrow\frac{\left(2m-2\right)^2-2.\left(m^2-m-5\right)}{m^2-m-5}=-\frac{10}{3}\)
\(\Leftrightarrow\frac{4m^2-8m+4-2m^2+2m+10}{m^2-m-5}=\frac{-10}{3}\)
\(\Leftrightarrow\left(2m^2-6m+14\right).3=-10.\left(m^2-m-5\right)\)
\(\Leftrightarrow6.\left(m^2-3m+7\right)=-10.\left(m^2-m-5\right)\)
\(\Leftrightarrow-3m^2+9m-21=5m^2-5m-25\)
\(\Leftrightarrow-3m^2+9m-21-5m^2+5m+25=0\)
\(\Leftrightarrow-8m^2+14m+4=0\)
\(\Leftrightarrow4m^2-7m-2=0\) \(\left(2\right)\)
từ PT (2) có \(\Delta=\left(-7\right)^2-4.4.\left(-2\right)=49+32=81>0\Rightarrow\sqrt{\Delta}=9\)
vì \(\Delta>0\) nên PT có 2 nghiệm phân biệt
\(m_1=\frac{7-9}{8}=\frac{-1}{4}\) ( TM ĐK
\(m_2=\frac{7+9}{8}=2\) \(m< 6\)và \(m^2-m-5\ne0\))
Bài này bạn áp dụng vi-ét là ra ngay nha !
Chúc bạn học tốt !
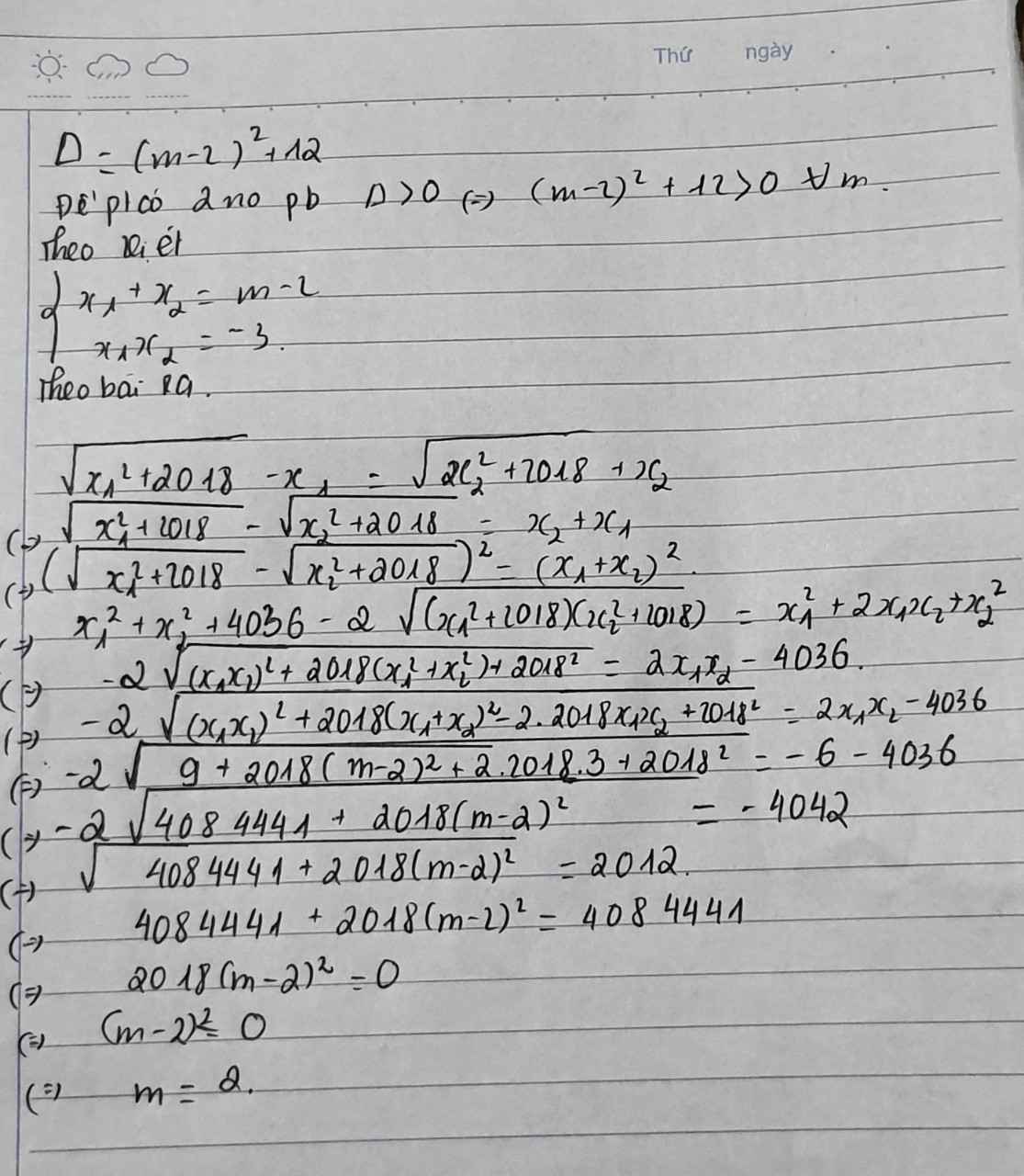
Để pt có 2 nghiệm phân biệt khi \(\Delta>0\)
hay \(\left(2m+1\right)^2-4.\left(-3\right)=\left(2m+1\right)^2+12>0\forall m\)
Vậy ta có đpcm