Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

e: =>-3<5x-12<3
=>9<5x<15
=>9/5<x<3
f: =>3x+15>=3 hoặc 3x+15<=-3
=>3x>=-12 hoặc 3x<=-18
=>x<=-6 hoặc x>=-4
b: =>(2x-7)(x-5)<=0
=>7/2<=x<=5

Vì 3 ≤ x ≤ 7 => x - 3 ≥ 0; 7 - x ≥ 0
=> C ≥ 0
Dấu = xảy ra khi và chỉ khi x = 3 hoặc x = 7
C = (x - 3)(7 - x) ≤ \(\dfrac{1}{4}\)(x - 3 + 7 - x)2 = \(\dfrac{1}{4}\).42 = 4
Dấu "=" xảy ra <=> x - 3 = 7 - x <=> x = 5
\(G=\left(x^2+\sqrt[3]{3}\right)+\left(\dfrac{2}{x^3}+\dfrac{2}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\ge2\sqrt{x^2.\sqrt[3]{3}}+3\sqrt[3]{\dfrac{2}{x^3}.\dfrac{2}{\sqrt{3}}.\dfrac{2}{\sqrt{3}}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}=2\sqrt[6]{3}.x+\dfrac{6}{\sqrt[3]{3}x}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\ge2\sqrt{2\sqrt[6]{3}.x.\dfrac{6}{\sqrt[3]{3}x}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}=2\sqrt{\dfrac{12\sqrt[6]{3}}{\sqrt[3]{3}}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\)
Dấu "=" xảy ra khi và chỉ khi \(x=\sqrt[6]{3}\)

\(f\left(-2\right)-f\left(1\right)=\left(-2\right)^2+2+\sqrt{2-\left(-2\right)}-\left(1^2+2+\sqrt{2-1}\right)\) \(=8-4=4\).
\(f\left(-7\right)-g\left(-7\right)=\left(-7\right)^2+2+\sqrt{2-\left(-7\right)}-\left(-2.\left(-7\right)^3-3.\left(-7\right)+5\right)=-658\)

a) Ta lập bảng xét dấu
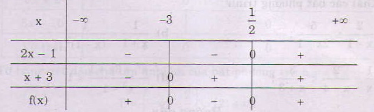
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪
a) Xét f(u) = \(\dfrac{u^p}{p}+\dfrac{v^q}{q}-uv,u\ge0\)
( Xem v > 0 vì v = 0 : BĐT luôn đúng )
f '(u) = up-1 - v = 0 \(\Leftrightarrow\) up-1 = v \(\Leftrightarrow\) u = \(v^{\dfrac{q}{p}}\)
Vẽ bảng biến thiên ( tự vẽ )
Vậy \(uv\le\dfrac{u^p}{p}+\dfrac{v^q}{q}\)
b)* Nếu \(\int\limits^b_a\left|f\left(x\right)\right|^pdx=0\) hay \(\int\limits^b_a\left|g\left(x\right)\right|^qdx=0\)thì \(f\equiv0\)hay \(g\equiv0\) BĐT luôn đúng
Xét \(\int\limits^b_a\left|f\left(x\right)\right|^pdx>0\) và \(\int\limits^b_a\left|g\left(x\right)\right|^qdx>0\)
Áp dụng BĐT câu (a) :
Với \(\left\{{}\begin{matrix}u=\dfrac{\left|f\left(x\right)\right|}{\left(\int\limits^b_a\left|f\left(x\right)\right|^pdx\right)^{\dfrac{1}{p}}}>0\\v=\dfrac{\left|g\left(x\right)\right|}{\left(\int\limits^b_a\left|g\left(x\right)\right|^qdx\right)^{\dfrac{1}{q}}}>0\end{matrix}\right.\)
\(uv\le\dfrac{u^p}{p}+\dfrac{v^q}{q}\left(1\right)\)
Lấy tích phân từ a \(\rightarrow\) b 2 vế BĐT (1) ta được :
\(\int\limits^b_auvdx\le\dfrac{1}{p}+\dfrac{1}{q}=1\)
Vậy : \(\int\limits^b_a\left|f\left(x\right).g\left(x\right)\right|dx\le\left(\int\limits^b_a\left|f\left(x\right)^p\right|dx\right)^{\dfrac{1}{p}}\left(\int\limits^b_a\left|g\left(x\right)^q\right|dx\right)^{\dfrac{1}{q}}\)
\(\Rightarrow\)(Đpcm )