Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) bạn dùng dấu U
điều kiện \(\begin{cases}m\ne0,m>-\frac{1}{4}\\m< 1\end{cases}\)
muons dễ nhìn thì vẽ trục số: 0 -1/4 1 x
=> điều kiện x \(\in\left(-\frac{1}{4};1\right)\backslash\left\{0\right\}\)

Câu 1:
Để ý rằng \((2-\sqrt{3})(2+\sqrt{3})=1\) nên nếu đặt
\(\sqrt{2+\sqrt{3}}=a\Rightarrow \sqrt{2-\sqrt{3}}=\frac{1}{a}\)
PT đã cho tương đương với:
\(ma^x+\frac{1}{a^x}=4\)
\(\Leftrightarrow ma^{2x}-4a^x+1=0\) (*)
Để pt có hai nghiệm phân biệt \(x_1,x_2\) thì pt trên phải có dạng pt bậc 2, tức m khác 0
\(\Delta'=4-m>0\Leftrightarrow m< 4\)
Áp dụng hệ thức Viete, với $x_1,x_2$ là hai nghiệm của pt (*)
\(\left\{\begin{matrix} a^{x_1}+a^{x_2}=\frac{4}{m}\\ a^{x_1}.a^{x_2}=\frac{1}{m}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a^{x_2}(a^{x_1-x_2}+1)=\frac{4}{m}\\ a^{x_1+x_2}=\frac{1}{m}(1)\end{matrix}\right.\)
Thay \(x_1-x_2=\log_{2+\sqrt{3}}3=\log_{a^2}3\) :
\(\Rightarrow a^{x_2}(a^{\log_{a^2}3}+1)=\frac{4}{m}\)
\(\Leftrightarrow a^{x_2}(\sqrt{3}+1)=\frac{4}{m}\Rightarrow a^{x_2}=\frac{4}{m(\sqrt{3}+1)}\) (2)
\(a^{x_1}=a^{\log_{a^2}3+x_2}=a^{x_2}.a^{\log_{a^2}3}=a^{x_2}.\sqrt{3}\)
\(\Rightarrow a^{x_1}=\frac{4\sqrt{3}}{m(\sqrt{3}+1)}\) (3)
Từ \((1),(2),(3)\Rightarrow \frac{4}{m(\sqrt{3}+1)}.\frac{4\sqrt{3}}{m(\sqrt{3}+1)}=\frac{1}{m}\)
\(\Leftrightarrow \frac{16\sqrt{3}}{m^2(\sqrt{3}+1)^2}=\frac{1}{m}\)
\(\Leftrightarrow m=\frac{16\sqrt{3}}{(\sqrt{3}+1)^2}=-24+16\sqrt{3}\) (thỏa mãn)
Câu 2:
Nếu \(1> x>0\)
\(2017^{x^3}>2017^0\Leftrightarrow 2017^{x^3}>1\)
\(0< x< 1\Rightarrow \frac{1}{x^5}>1\)
\(\Rightarrow 2017^{\frac{1}{x^5}}> 2017^1\Leftrightarrow 2017^{\frac{1}{x^5}}>2017\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}> 1+2017=2018\) (đpcm)
Nếu \(x>1\)
\(2017^{x^3}> 2017^{1}\Leftrightarrow 2017^{x^3}>2017 \)
\(\frac{1}{x^5}>0\Rightarrow 2017^{\frac{1}{x^5}}>2017^0\Leftrightarrow 2017^{\frac{1}{5}}>1\)
\(\Rightarrow 2017^{x^3}+2017^{\frac{1}{x^5}}>2018\) (đpcm)

câu 1 sao không ra đáp án nào vậy bạn , hình như bạn làm sai đâu đó rồi
Trời, đọc xong chỉ việc chọn đáp án mà ko biết chọn luôn?
Đáp án D chứ sao nữa

Câu 2:
$y'=-3x^2+6x+(m-2)=0$
Để hàm số có 2 điểm cực trị $x_1,x_2$ đồng nghĩa với PT $-3x^2+6x+(m-2)=0$ có 2 nghiệm phân biệt $x_1,x_2$
$\Leftrightarrow \Delta'=9+3(m-2)>0\Leftrightarrow m>-1(1)$
Hai điểm cực trị cùng dương khi:
\(\left\{\begin{matrix} x_1+x_2=2>0\\ x_1x_2=\frac{m-2}{-3}>0\end{matrix}\right.\Leftrightarrow m< 2(2)\)
Từ $(1);(2)\Rightarrow -1< m< 2$
Đáp án C.
Câu 2:
Để đths có 2 điểm cực trị thì trước tiên:
$y'=x^2-2mx+m^2-4=0$ có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi $\Delta'=m^2-(m^2-4)>0\Leftrightarrow m\in\mathbb{R}$
Để 2 điểm cực trị của đồ thị $y$ nằm về hai phía của trục tung thì: $x_1x_2< 0$
$\Leftrightarrow m^2-4< 0$
$\Leftrightarrow -2< m< 2$
Đáp án A.

Đáp án A
Ghi nhớ: Nếu hàm số ![]()
liên tục trên đoạn ![]() và
và ![]() thì phương trình
thì phương trình ![]()
có ít nhất một nghiệm nằm trong khoảng ![]() .
.

Ta có x3 - 3x2 + 1 - m = 0 (1) là phương trình hoành độ giao điểm giữa hai đồ thị hàm số y = x3-3x2+1 và y = m (là đường thẳng song song hoặc trùng với Ox).
Xét y = x3-3x2+1 .
Tính y’ = 3x2- 6x
Ta có
y ' = 0 ⇔ 3 x 2 - 6 x = 0 ⇔
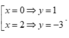
Ta có x = 1 thì y = -1
Số nghiệm của phương trình chính là số giao điểm của đồ thị y = x3-3x2+1 và đường thẳng y = m .
Do đó, yêu cầu bài toán khi và chỉ khi -3 < m < -1
Chọn C.