Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình có nghiệm kép khi m ≠ -2 và Δ = 0.
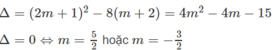
Khi m = 5/2 nghiệm kép của phương trình là
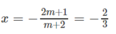
Khi m = -3/2 nghiệm kép của phương trình là x = 2.

Để phương trình có hai nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}\Delta\ge0\\a\ne0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(3m-1\right)^2-4.\left(m+1\right)\left(2m-2\right)\ge0\\\Delta\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+9\ge0\\m\ne-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-3\right)^2\ge0\\m\ne1\end{matrix}\right.\)\(\Leftrightarrow m\ne1\).
Áp dụng định ly Viet:
\(x_1+x_2=-\dfrac{3m-1}{m+1}=3\)\(\Leftrightarrow3m-1=-3m-3\)\(\Leftrightarrow6m=-2\)\(\Leftrightarrow m=-\dfrac{1}{3}\).
Vậy \(m=-\dfrac{1}{3}\) là giá trị cần tìm.

\(\Leftrightarrow2m.2^x+\left(2m+1\right)\left(3-\sqrt{5}\right)^x+\left(3+\sqrt{5}\right)^x=0\)
\(\Leftrightarrow\left(\frac{3+\sqrt{5}}{2}\right)^x+\left(2m+1\right)\left(\frac{3-\sqrt{5}}{2}\right)^x+2m< 0\)
Đặt \(t=\left(\frac{3+\sqrt{5}}{2}\right)^x,0< t\le1\Rightarrow\frac{1}{t}=\left(\frac{3-\sqrt{5}}{2}\right)^x\)
Phương trình trở thành :
\(t+\left(2m+1\right)\frac{1}{t}+2m=0\) (*)
a. Khi \(m=-\frac{1}{2}\) ta có \(t=1\) suy ra \(\left(\frac{3+\sqrt{5}}{2}\right)^x=1\Leftrightarrow x=0\)
Vậy phương trình có nghiệm là \(x=0\)
b. Phương trình (*) \(\Leftrightarrow t^2+1=-2m\left(t+1\right)\Leftrightarrow\frac{t^2+1}{t+1}=-2m\)
Xét hàm số \(f\left(t\right)=\frac{t^2+1}{t+1};t\in\)(0;1]
Ta có : \(f'\left(t\right)=\frac{t^2+2t+1}{\left(t+1\right)^2}\Rightarrow f'\left(t\right)=0\Leftrightarrow=-1+\sqrt{2}\)
t f'(t) f(t) 0 1 0 - + 1 1 -1 + căn 2 2 căn 2 - 2
Suy ra phương trình đã cho có nghiệm đúng
\(\Leftrightarrow2\sqrt{2}-2\le-2m\le1\Leftrightarrow\sqrt{2}-1\ge m\ge-\frac{1}{2}\)
Vậy \(m\in\left[-\frac{1}{2};\sqrt{2}-1\right]\) là giá trị cần tìm

a)
ĐIều kiện (1)\(\Delta>0\Rightarrow\left(m+3\right)^2-4\left(m^2-1\right)\left(m^2+m\right)>0\)
ĐK(2) c/a <0 => (m^2+m)/(m^2-1) <0
Không cần giải đk (1) vì nếu (m) thủa mãn đk(2) tất nhiên thỏa mãn đk(1) do (x+3)^2 >=0
\(\dfrac{m^2+m}{m^2-1}=\dfrac{T}{M}\)
\(-1< m< 0\Rightarrow T< 0\)
\(-1< m< 1\Rightarrow M< 0\)
Để thủa mãn đk (2) cũng là giá trị m cần tìm là: \(\Rightarrow0< m< 1\)
b)
M thả mãn hệ \(\left\{{}\begin{matrix}\left(m^3+m-2\right)^2-4\left(m^2+m-5\right)\left(1\right)\\\left(m^2+m-5\right)< 0\left(2\right)\end{matrix}\right.\)
Tưng tự câu (a) Nếu (2) thủa mãn => ( 1) thỏa mãn
=> \(\left(2\right)\Rightarrow\dfrac{-1-\sqrt{21}}{2}< m< \dfrac{-1+\sqrt{21}}{2}\) cũng là giá trị m cần tìm

Phương trình có hai nghiệm trái dấu khi và chỉ khi ![]() suy ra m < -2.
suy ra m < -2.
Tổng của hai nghiệm bằng -3 khi ![]() thỏa mãn điều kiện m < -2.
thỏa mãn điều kiện m < -2.
Đáp số: m = -5.


a) Để phương trình có hai nghiệm trái dấu khi và chỉ khi: \(ac< 0\Leftrightarrow2\left(m+2\right)< 0\)\(\Leftrightarrow m+2< 0\)\(\Leftrightarrow m< -2\). (1)
Tổng hai nghiệm đó bằng - 3 khi và chỉ khi:
\(x_1+x_2=\dfrac{2m+1}{m+2}=-3\)
\(\Rightarrow2m+1=3\left(m+2\right)\)\(\Leftrightarrow m=-5\)
Kết hợp với điều kiện (1) ta được \(m=-5\) là giá trị cần tìm.
b) Phương trình có nghiệm kép khi và chỉ khi:
\(\left\{{}\begin{matrix}a\ne0\\\Delta=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+2\ne0\\\left(2m+1\right)^2-4.2.\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\end{matrix}\right.\)
Vậy \(m=\dfrac{5}{2}\) hoặc \(m=-\dfrac{3}{2}\) là giá trị cần tìm.