Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(A=\dfrac{3}{n+2}\left(\forall n\in Z\right)\)
a) Để \(A\) là phân số thì \(n+2\ne0\Leftrightarrow n\ne-2\)
Vậy \(n\ne-2\) thì \(A\) là phân số.
b) Thay \(n=0;n=2;n=-7\) lần lượt vào \(A\) ta có:
\(\left\{{}\begin{matrix}A=\dfrac{3}{0+2}=\dfrac{3}{2}\\A=\dfrac{3}{2+2}=\dfrac{3}{4}\\A=\dfrac{3}{-7+2}=\dfrac{-3}{5}\end{matrix}\right.\)
c) Để \(A\in Z\Rightarrow\left(n+2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-1;-3;1;-5\right\}\)
Vậy \(n\in\left\{-1;-3;1;-5\right\}\) thì \(A\in Z\)

a) A là phân số khi n+6 là số nguyên khác 0
\(\Rightarrow n\ne-6\)
Vậy n là số nguyên khác -6.
b) Với n=2, ta có : \(\frac{-3}{n+6}=\frac{-3}{2+6}=\frac{-3}{8}\)
Với n=4, ta có : \(\frac{-3}{n+6}=\frac{-3}{4+6}=\frac{-3}{10}\)
c) A là số nguyên khi -3\(⋮\)n+6
\(\Rightarrow n+6\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow n\in\left\{-7;-5;-9;-3\right\}\)
a)Để A là phân số thì \(n+6\ne0\Leftrightarrow n\ne-6\)
Vậy để A là phân số thì \(n\ne-6\)
b) Thay n=2(tm) vào A, ta có:
\(A=\frac{-3}{2+6}=\frac{-3}{8}\)
Thay n=4 (tm) vào A, ta có:
\(A=\frac{-3}{4+6}=\frac{-3}{10}\)
c) Để A là số nguyên \(\Rightarrow\frac{-3}{n+6}\)là số nguyên
\(\Rightarrow n+6\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\)
Ta có bảng giá trị
| n+6 | -3 | -1 | 1 | 3 |
| n | -9 | -7 | -5 | -3 |

a) HS tự làm.
b) HS tự làm.
c) Phân số A có giá trị là số nguyên khi (n + 5):(n + 4) Từ đó suy ra l ⋮ (n + 4) hay n + 4 là ước của 1.
Do đó n ∈ (-5; -3).

\(A=\frac{4}{2n-1}\)
a, ĐK : \(2n-1\ne0\Leftrightarrow n\ne\frac{1}{2}\)
b, Khi n = 0
\(A=\frac{4}{2.0-1}=\frac{4}{0-1}=\frac{4}{-1}=-4\)
Khi n = 3
\(A=\frac{4}{2.3-1}=\frac{4}{6-1}=\frac{4}{5}\)
Khi n = 5
\(A=\frac{4}{2.5-1}=\frac{4}{10-1}=\frac{4}{9}\)
c, Để \(A\in Z\)thì \(4⋮2n-1\)hay \(2n-1\inƯ\left(4\right)\)
Ta có bảng sau :
| Ư(4) | 2n-1 | n |
| 1 | 1 | 1 ( TM) |
| -1 | -1 | 0 ( TM ) |
| 2 | 2 | 3/2 ( Loại ) |
| -2 | -2 | -1/2 ( Loại ) |
| 4 | 4 | 5/2 ( Loại ) |
| -4 | -4 | -3/2 ( Loại ) |
Vậy để A nguyên thì \(n\in\left\{1;0\right\}\)

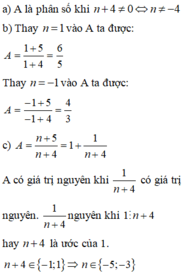
gfvfvfvfvfvfvfv555