Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Vì (P) đi qua M(4;3) nên 3= 16a+ 4b+c (1)
Mặt khác (P) cắt Ox tại N(3;0) suy ra 0=9a+3b+c (2) , (P) cắt Ox tại P nên P(t; 0) với 0= at2+ bt+c (*) ; (P) cắt Ox tại N và P nên phương trình (*) có 1 nghiệm là t=3 ( hoành độ điểm N)
Từ (1) và (2); vế trừ vế ta có 7a+ b=3 hay b= 3-7a
suy ra: 
Thay vào (3) ta có:
Suy ra a= 1; b= -4; c=3.
Vậy (P) cần tìm là y= x2-4x+3.
Chọn B.
Từ điều kiện đề bài: (hiển nhiên a khác 0):
\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=-1\\a-b+c=7\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a-b^2=-4a\\a-b=6\\c=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-6\right)^2-8a=0\\b=a-6\\c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\left\{2;18\right\}\\b=a-6\\c=1\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=2x^2-4x+1\\y=18x^2+12x+1\end{matrix}\right.\)
+ Parabol y = ax2 + bx + 2 đi qua M(1 ; 5)
⇒ 5 = a.12 + b.1 + 2 ⇒ a + b = 3 (1) .
+ Parabol y = ax2 + bx + 2 đi qua N(–2; 8)
⇒ 8 = a.( –2)2 + b.( –2) + 2 ⇒ 4a – 2b = 6 (2).
Từ (1) và (2) suy ra: a = 2; b = 1.
Vậy parabol cần tìm là y = 2x2 + x + 2.
1/ Do (P) qua A \(\Rightarrow c=1\) (thay tọa độ A vào pt (P) thôi)
(P) có đỉnh nằm trên trục hoành
\(\Rightarrow-\frac{\Delta}{4a}=0\Rightarrow\Delta=0\Rightarrow b^2-4ac=0\Rightarrow b^2=4ac=4a\Rightarrow a=\frac{b^2}{4}\)
Do (P) qua B \(\Rightarrow4a+2b+c=1\Rightarrow b^2+2b=0\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow a=0\left(l\right)\\b=-2\Rightarrow a=1\end{matrix}\right.\)
2/ Cần tìm 3 ẩn mà chỉ cho 1 dữ liệu, how to giải?
3/ \(-\frac{b}{2a}=2>1>-2\) và \(a=1>0\)
\(\Rightarrow\) hàm số nghịch biến trên \(\left[-2;1\right]\)
\(\Rightarrow y_{max}=y\left(-2\right)=15\)
Vì parabol đi qua ba điểm A, B, C nên ta có hệ phương trình:
Vậy (P): y = -x2 + 2x
Chọn C.
(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình 
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.
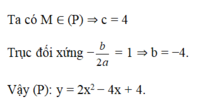
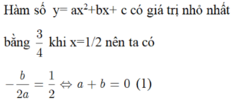
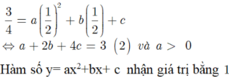
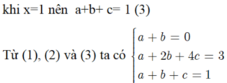
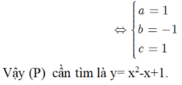
Từ đề bài \(\Rightarrow a>0\) và:
\(\left\{{}\begin{matrix}\frac{4ac-b^2}{4a}=-5\\a+b+c=-1\\c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b^2=36a\\a+b=-5\\c=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\frac{b^2}{36}\\\frac{b^2}{36}+b+5=0\\c=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=-6\\c=4\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}a=25\\b=-30\\c=4\end{matrix}\right.\)