Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)

+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
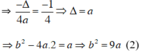
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.

(P) đi qua điểm B(-1;6) nên ta có PT: 6=a-b+2 => a=4+b (1)
hàm số có tung độ đỉnh là -1/4 nên: (-b^2+4*2*a)/4a=-1/4
=>-4a=-4b^2+32a =>4b^2-36a=0 => b^2-9a=0 (2)
thay (1) vào (2)=> b=12 hoặc b=-3
=>a=16 hoặc a=1 => (a;b)=(16;12) (thoả mãn)
hoặc (a;b)=(1;-3) (thoả mãn)

Lời giải:
Theo bài ra thì tọa độ đỉnh của parabol là $(-2,19)$
Từ hàm $y=ax^2+bx+3=a(x+\frac{b}{2a})^2+3-\frac{b^2}{4a}$ ta có tọa độ đỉnh của parabol là:
$(\frac{-b}{2a}, 3-\frac{b^2}{4a})$
$\Rightarrow \frac{-b}{2a}=-2; 3-\frac{b^2}{4a}=19$
$\Rightarrow a=-4; b=-16$

\(\left\{{}\begin{matrix}\dfrac{4ac-b^2}{4a}=1\\4a+2b+c=0\\4a-2b+c=-8\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4ac-b^2=4a\\4a+2b+c=0\\4b=8\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=2\\4ac-4=4a\\4a+4+c=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=2\\ac-1=a\\c=-4a-4\end{matrix}\right.\)
\(\Rightarrow a\left(-4a-4\right)-1=a\)
\(\Rightarrow4a^2+5a+1=0\) \(\Rightarrow\left[{}\begin{matrix}a=-1\Rightarrow c=0\\a=-\dfrac{1}{4}\Rightarrow c=-3\end{matrix}\right.\)
Vậy có 2 pt (P): \(\left[{}\begin{matrix}y=-x^2+2x\\y=-\dfrac{1}{4}x^2+2x-3\end{matrix}\right.\)

Parabol đi qua điểm M suy ra 6 = 25a – 5b + c (1)
Parabol cắt Oy tại điểm có tung độ bằng -2 nên -2 = a.0 + b.0 + c hay c = -2
Vậy 25a – 5b = 8
Chọn B.

a) Thay x=1 và y=-2 vào (P), ta được:
\(a\cdot1^2-4\cdot1+c=-2\)
\(\Leftrightarrow a-4+c=-2\)
hay a+c=-2+4=2
Thay x=2 và y=3 vào (P), ta được:
\(a\cdot2^2-4\cdot2+c=3\)
\(\Leftrightarrow4a-8+c=3\)
hay 4a+c=11
Ta có: \(\left\{{}\begin{matrix}a+c=2\\4a+c=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3a=-9\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\c=2-a=2-3=-1\end{matrix}\right.\)
Vậy: (P): \(y=3x^2-4x-1\)
THam khảo
Bài 2:
Ta có: −Δ4a=−3−Δ4a=−3
⇔−Δ=−12a⇔−Δ=−12a
⇔b2−4a=12a⇔b2−4a=12a
⇔b2−16a=0(1)⇔b2−16a=0(1)
Thay x=-1 và y=6 vào (P), ta được:
a⋅(−1)2+b(−1)+1=6a⋅(−1)2+b(−1)+1=6
⇔a−b=5⇔a−b=5
⇔a=b+5⇔a=b+5(2)
Thay (2) vào (1), ta được:
b2−16(b+5)=0b2−16(b+5)=0
⇔b2−16b+64−144=0⇔b2−16b+64−144=0
⇔(b−8)2=144⇔(b−8)2=144
⇔[b=20b=−4⇔[a=25a=1
giúp mình câu mới nhất ạ