Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 :
M A C D E F N K O B
a.Ta có MC là tiếp tuyến của (O)
\(\Rightarrow MC\perp OC\)
Mà \(MK\perp KD\Rightarrow\widehat{MCO}=\widehat{MKD}=90^0\Rightarrow OCDK\) nội tiếp
b.Vì MC là tiếp tuyến của (O)
\(\Rightarrow\widehat{MCA}=\widehat{MBC}\Rightarrow\Delta MCA~\Delta MBC\left(g.g\right)\)
\(\Rightarrow\frac{MC}{MB}=\frac{MA}{MC}\Rightarrow MC^2=MA.MB\)
c . Vì MO∩(O)=AB \(\Rightarrow AB\) là đường kính của (O)
\(\Rightarrow AC\perp BC\Rightarrow\widehat{BCD}+\widehat{MCA}=90^0\Rightarrow\widehat{BCD}=90^0-\widehat{MCA}\)
Mà \(\widehat{MCA}=\widehat{MBC}\Rightarrow\widehat{MCD}=90^0-\widehat{ABN}=\widehat{BNK}=\widehat{CND}\)
\(\Rightarrow\Delta DCN\) cân
d ) Ta có : \(\widehat{BFD}=90^0=\widehat{BKD}\) vì AB là đường kính của (O)
\(\Rightarrow BKFD\) nội tiếp
\(\Rightarrow\widehat{FDK}=\widehat{KBF}=\widehat{ABC}+\widehat{CBF}=\widehat{MCA}+\widehat{FCD}=\widehat{DCE}\)
\(+\widehat{FCD}=\widehat{FCE}\)
Vì MC là tiếp tuyến của (O)
\(\Rightarrow CEDF\) nội tiếp

1) Ta có \(\widehat{ABO}=\widehat{ACO}=90độ\left(gt\right)\)
Do đó\(\widehat{ABO}+\widehat{ACO}=180độ\)
Nên tứ giác ABOC nội tiếp đường tròn đường kính AO
Tâm đường tròn ngoại tiếp tứ giác ABOC là trung điểm AO.
2) Xét ΔABD và ΔAEB có
\(\widehat{BAE}\)chung
\(\widehat{ABD}=\widehat{AEB}\)(góc tạo bởi tia tiếp tuyến và dây và góc nội tiếp cùng chắn \(\widebat{BD}\))
Nên ΔABD 
Do đó \(\frac{AB}{AE}\)=\(\frac{AD}{AB}\)
Hay AB2= AE.AD

a) Ta có: \(\widehat{OBA}+\widehat{OCA}=90^o\)
=> OBAC nội tiếp
b) Xét tam giác AEB và tam giác ABD
Có: \(\widehat{BAD}\)chung
\(\widehat{ADB}=\widehat{ABE}=\frac{1}{2}sđ\widebat{BE}\)
=> Tam giác AEB đồng dạng tam giác ABD (g.g)
=> \(\frac{AE}{AB}=\frac{AB}{AD}\)=>AB2=AE.AD (đpcm)
c) Kẽ BE cắt AC tại S
CE cắt AB tại P
Ta có:\(\hept{\begin{cases}\widehat{BEP}=\widehat{CES}=\frac{1}{2}sđ\widebat{BC}\\\widehat{AEP}=\widehat{CED}=\frac{1}{2}sđ\widebat{CD}\end{cases}}\)(1)
Mặt khác: \(\hept{\begin{cases}\widehat{BDC}=\widehat{BCA}=\frac{1}{2}sđ\widebat{BC}\\\widehat{DBC}=\widehat{BCA}\left(slt\right)\end{cases}}\)
=> \(\widehat{BDC}=\widehat{DBC}\)
=> Tam giác BDC cân tại C
=> CD=BC
=> \(\widebat{CD}=\widebat{BC}\)(2)
Từ (1),(2) => \(\widehat{BEP}=\widehat{AEP}\)
=> Tia đổi của tia EC là tia phân giác của góc BEA

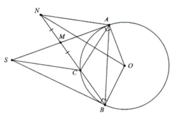
a, S A O ^ + S B O ^ = 90 0 + 90 0 = 180 0
Tứ giác OASB nội tiếp
b, M A C ^ = C B A ^ = 1 2 s đ C A ⏜
=> ∆MAC:∆MBA(g.g)
Từ đó suy ra M A 2 = M B . M C
c, Có M A 2 = M B . M C mà MA = MS => S M M S = M C M S
Chứng minh được ∆MSB:∆MCS
=>
M
B
S
^
=
C
S
M
^
hay
M
B
S
^
=
C
S
A
^
d, Chứng minh
N
A
S
^
=
M
B
S
^
(Vì cùng =
C
S
A
^
)
=> Tứ giác NAOB là từ giác nội tiếp
Chứng minh được A N O ^ = O N B ^
=> ĐPCM
a: Xét tứ giác SAOB có \(\widehat{SAO}+\widehat{SBO}=90^0+90^0=180^0\)
nên SAOB là tứ giác nội tiếp
b:
Xét ΔSAO vuông tại A có \(SA^2+AO^2=SO^2\)
=>\(SA^2=8^2-4^2=48\)
=>\(SA=4\sqrt{3}\left(cm\right)\)
Xét ΔSAO vuông tại A có \(sinASO=\dfrac{AO}{OS}=\dfrac{1}{2}\)
nên \(\widehat{ASO}=30^0\)
Xét (O) có
SA,SB là các tiếp tuyến
Do đó: SO là phân giác của góc ASB và SA=SB
=>\(\widehat{ASB}=2\cdot\widehat{ASO}=60^0\)
Xét ΔSAB có SA=SB và \(\widehat{ASB}=60^0\)
nên ΔSAB đều
=>\(AB=SA=4\sqrt{3}\left(cm\right)\)