Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔOBC cân tại O
mà OH là đường cao
nên H là trung điểm của BC
=>HB=HC=24/2=12cm
ΔOHB vuông tại H
=>\(OH^2+HB^2=OB^2\)
=>\(OH^2+12^2=15^2\)
=>\(OH^2=15^2-12^2=81\)
=>OH=9(cm)
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ΔOBC cân tại O
mà OH là đường trung tuyến
nên OH là đường trung trực của BC(2)
Từ (1),(2) suy ra O,H,A thẳng hàng
c:Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
=>\(OA=\dfrac{OB^2}{OH}=\dfrac{15^2}{9}=25\left(cm\right)\)
ΔOBA vuông tại B
=>\(OB^2+BA^2=OA^2\)
=>\(BA^2+15^2=25^2\)
=>\(BA^2=625-225=400\)
=>BA=20(cm)
AB=AC
mà AB=20cm
nên AC=20cm
d: Xét ΔOBM vuông tại B và ΔOCN vuông tại C có
OB=OC
\(\widehat{BOM}=\widehat{CON}\)
Do đó: ΔOBM=ΔOCN
=>BM=CN
Xét ΔAMN có \(\dfrac{AB}{BM}=\dfrac{AC}{CN}\)
nên BC//MN
AB+BM=AM
AC+CN=AN
mà AB=AC và BM=CN
nên AM=AN
=>\(\widehat{BMN}=\widehat{CNM}\)
Xét tứ giác BCNM có BC//MN
nên BCNM là hình thang
Hình thang BCNM có \(\widehat{BMN}=\widehat{CNM}\)
nen BCNM là hình thang cân

Tự vẽ hình
a) theo t/c 2 tiếp tuyến cắt nhau
=> AB =AC
mà OB =OC =R
=> OA là trung trực của BC => OA vuông góc BC tại H => H là trung điểm của BC => BH =BC/2 =15
Áp dụng Pi - ta -go cho HBO vuông tại H => OH2 = OB2 - BH2 = 172 - 152 =64 => OH =8
b) theo câu a => O;H;A thẳng hàng rồi
c)

a) Dùng Pytago ta tính được OH=9cmOH=9cm
b) Vì AB=AC và OB=OC=R nên OA là đường trung trực BC
Mà H là trung điểm BC
=>A,H,O=>A,H,O thẳng hàng.
c.\(\Delta ABO\) Vuông tại B đươngg cao BH
\(\Rightarrow\frac{1}{AB^2}=\frac{1}{BH^2}-\frac{1}{OB^2}\)
\(\Rightarrow\frac{1}{12^2}-\frac{1}{15^2}=\frac{1}{400}\)
\(\Rightarrow AB=20cm\)

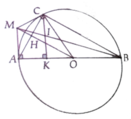
a, HS tự làm
b, HS tự làm
c, IK = 1 2 CK = 1 2 AC.sinα = R.cosα.sinα
d, Giả sử BI cắt AM tại N. Vì IK//AM => MO = OP
=> 1 O I 2 = 1 O M 2 + 1 O N 2
= 1 O P 2 + 1 O N 2 = 1 O B 2 => M ≡ N

DC = DA
OA = OC
Do đó OD là trung trực của đoạn thẳng AC : suy ra OD vuông góc với AC
Tứ giác OECH có góc CEO + góc CHO = 180 độ
Suy ra tứ giác OECH là tứ giác nội tiếp


