Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

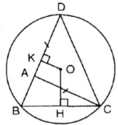
Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)

tham khảo
a)Ta có: AC//BD(gt)
OH⊥AC(gt)
Do đó: OH⊥BD(Định lí 2 từ vuông góc tới song song)
Ta có: OH⊥BD(cmt)
OK⊥BD(gt)
mà OH và OK có điểm chung là O
nên H,O,K thẳng hàng(đpcm)
b) Vì đường tròn (O) có AB là đường kính(gt)
nên O là trung điểm của AB
hay OA=OB
Xét ΔAOH vuông tại H và ΔBOK vuông tại K có
OA=OB(cmt)
gocAOH=gocBOK(hai góc đối đỉnh)
Do đó: ΔAOH=ΔBOK(cạnh huyền-góc nhọn)
⇒AH=BK(hai cạnh tương ứng)
c) Ta có: ΔAOH=ΔBOK(cmt)
nên OH=OK(hai cạnh tương ứng)
Vì đường tròn (O) có CD là dây
nên OC=OD
Xét ΔCOH vuông tại H và ΔDOK vuông tại K có
OC=OD(cmt)
OH=OK(cmt)
Do đó: ΔCOH=ΔDOK(cạnh huyền-cạnh góc vuông)
⇒HC=KD(hai cạnh tương ứng)
Ta có: AC=AH+HC(H nằm giữa A và C)
BD=BK+DK(K nằm giữa B và D)
mà AH=BK(cmt)
và HC=DK(cmt)
nên AC=BD(đpcm)

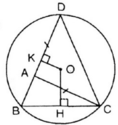
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)
Mà AD = AC (gt)
⇒ BC < AB + AD = BD
Mà OH là khoảng cách từ O đến dây BC
OK là khoảng cách từ O đến dây BD
⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)
b) Vì BD > BC
⇒ 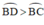
Kiến thức áp dụng
+ Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn
+ Trong một đường tròn, dây lớn hơn căng cung lớn hơn.

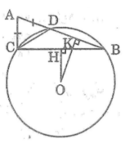
Áp dụng bất đẳng thức tam giác vào ΔABC , ta có: BC > AB - AC mà AC = AD (gt)
suy ra : BC > AB – AD hay : BC > BD
Vì trong một đường tròn ,dây cung lớn hơn gần tâm hơn nên: OH < OK


d(O;AC)=OH
d(O;BD)=OK
mà OH=OK
nên AC=BD
góc ACB=1/2*sđ cung AB=90 độ
Xét tứ giác ACBD có
AC//BD
AC=BD
=>ACBD là hình bình hành
mà góc ACB=90 độ
nên ACBD là hình chữ nhật