Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

O A B x C E D M
a, xét tg AEO và CEO có : EO chung
^AEO = ^CEO = 90
OA = OC = r
=> Tg AEO = tg CEO (ch-cgv)
=> ^AOE = ^COE
xét tg MAO và tg MCO có : Mo chung
OA = OC = r
=> tg MAO = tg MCO (cg-c)
=> ^MAO = ^MCO
mà ^MAO = 90
=> ^MCO = 90 => OC _|_ MC
có C thuộc 1/2(o)
=> MC là tt của 1/2(o)
b, xét tứ giác MCOA có : ^MCO = ^MAO = 90
=> ^MCO + ^MAO = 180
=>MCOA nội tiếp
+ có D thuộc 1/(o) dk AB (gt) => ^ADB = 90 = ADM
có MEA = 90 do AC _|_ MO (Gt)
=> ^ADM = ^MEA = 90
=> MDEA nt

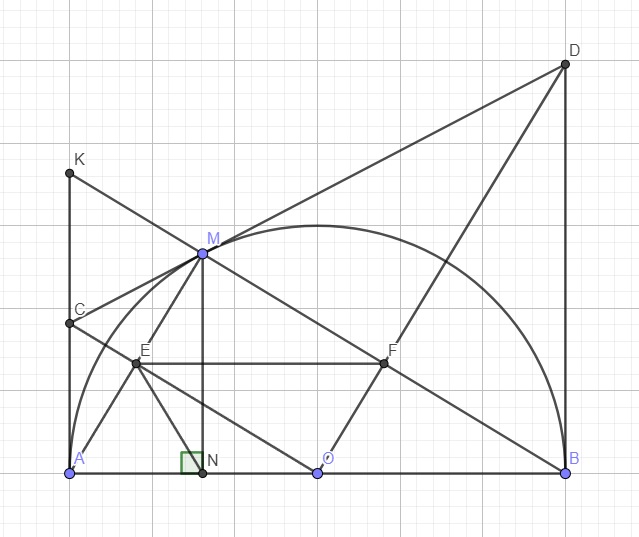
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân

GT : Nửa đường tròn tâm O đường kính AB , C thuộc nữa đường tròn , D nằm trên đoạn OA, tiếp tuyến Ax,By của nửa đường tròn . Qua C , đường thẳng vuông góc CD cắt tiếp tuyến Ax,By ở M và N ; AC cắt DM = {P} ; BC cắt DN = {Q}
KL : a) ADCM và BDCN nội tiếp đường tròn
b) Góc MDN = 90 độ
C . PQ//AB
Mik giải luôn nhé để nếu bạn cần thì có thể tham khảo luôn :
(Dưới đây là bài làm tham khảo , bạn có thể tham khảo nhé !)
Nguồn bài tham khảo nếu bạn muốn xem thêm cách làm khác :https://hoc24.vn/cau-hoi/cho-nua-duong-tron-tam-o-duong-kinh-ab-lay-diem-c-thuoc-nua-duong-tron-va-diem-d-tren-doan-oa-ve-cac-tiep-tuyen-axby-cua-nua-duong-tron-duong-than.222294491220

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: OC là tia phân giác của \(\widehat{AOM}\)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: OD là tia phân giác của \(\widehat{BOM}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{MOC}+\widehat{MOD}\right)=180^0\)
hay \(\widehat{COD}=90^0\)

a: Xét (O) có
CM là tiếp tuyến có M là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm
DB là tiếp tuyến có B là tiếp điểm
Do đó: DM=DB
Ta có: MC+MD=CD
mà MC=CA
và MD=DB
nên CD=AC+BD