Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

viết đề sai rùi bạn
b) chứng minh tứ giác POMQ LÀ hình chữ nhật chứ ko phải chứng minh AQMO LÀ HÌNH CHỮ NHẬT OK

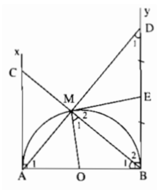
Tam giác EBM cân nên ∠ M 2 = ∠ B 2 . Suy ra ∠ M 1 + ∠ M 2 = ∠ B 1 + ∠ B 2 = 90 ° , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.

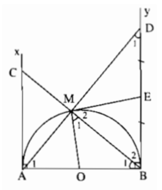
a) ∠ B 1 = ∠ D 1 (cùng phụ với ∠ A 1 ).
∆ ABC ∼ ∆ BDA (g.g) suy ra
AB/BD = AC/AB, do đó AC.BD = A B 2

Hình bạn tự vẽ nhé.
Xét \(\left(O\right)\) có
ΔABM nội tiếp đường tròn
AB là đường kính
Do đó: ΔABM vuông tại M
Xét ΔAMB có
O là trung điểm của AB
C là trung điểm của AM
Do đó: OC là đường trung bình của ΔAMB
Suy ra: OC//MB và \(OC=\dfrac{MB}{2}\)
mà D\(\in\)MB và \(MD=\dfrac{MB}{2}\)
nên OC//MD và OC=MD
Xét tứ giác MCOD có
OC//MD
OC=MD
Do đó: MCOD là hình bình hành
mà \(\widehat{M}=90^0\)
nên MCOD là hình chữ nhật