Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhận xét
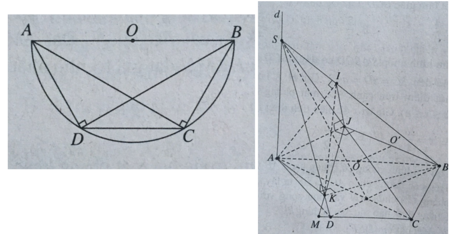
Hình thang ABCD có hai cạnh bên và đáy nhỏ bằng nhau và bằng nửa đáy lớn, nên nó là nửa lục giác đều nội tiếp trong đường tròn đường kính AB, tâm O là trung điểm của AB.
Như vậy: ∠(ACB) = ∠(ADB) = 1v.
a) Theo giả thiết, ta có: SA ⊥ (ABCD) ⇒ SA ⊥ BC
BC ⊥ SA & BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC. (1)
Mặt khác SB ⊥ (P) nên SB ⊥ IJ (⊂ (P)) (2)
Từ (1) và (2) suy ra BCJI là tứ giác nội tiếp trong đường tròn đường kính BJ.
Ta có BC ⊥ (SAC) ⇒ BC ⊥ AJ (⊂ (SAC))
AJ ⊥ BC & AJ ⊥ SB (do SB ⊥ (P)) ⇒ AJ ⊥ (SBC) ⇒ AJ ⊥ JI (⊂ (SBC)) (3)
Lý luận tương tự, ta có:
BD ⊥ AD & BD ⊥ SA ⇒ BD ⊥ (SAD) ⇒ BD ⊥ AK (⊂ (SAD))
AK ⊥ BD & AK ⊥ SB(⊂ (P)) ⇒ AK ⊥ (SBD) ⇒ AK ⊥ KI. (4)
Từ (3) và (4) suy ra AKJI nội tiếp trong đường tròn đường kính AI nằm trong mặt phẳng (P).
b) Ta có ngay O’ là trung điểm BJ
Vì OO’ là đường trung bình của ΔABJ nên OO’ // AJ
Mà AJ ⊥ (SBC) nên OO’ ⊥ (SBC)
c) Ta có (SCD) ∩ (ABCD) = CD.
Gọi M = JK ∩ CD
SA ⊥ (ABCD) ⇒ SA ⊥ AM(⊂ (ABCD)) (5)
SB ⊥ (P) ⇒ SB ⊥ AM (⊂ (P)) (6)
Từ (5) và (6), ta có: AM ⊥ (SAB) ⇒ AM ⊥ AB.
Suy ra AM là tiếp tuyến của đường tròn ngoại tiếp ΔABC tại A. Như vậy AM cố định. Vì M = AM ∩ CD nên M cố định.
d) ΔAIB vuông tại I nên OA = OB = OI
ΔAJB vuông tại J (do AJ ⊥ (SBC)) nên OA = OB = OJ).
ΔAKB vuông tại K (do AK ⊥ (SBD)) nên OA = OB = OK).
Ta có OA = OB = OC = OD = OI = OJ = OK nên O là điểm cách đều các điểm đã cho và OA = AB/2 = a.
e) Theo chứng minh câu c.
f) Khi S thay đổi trên d, ta có I luôn nằm trong mặt phẳng (B, d).
Trong mặt phẳng này I luôn nhìn đoạn AB cố định dưới góc vuông nên tập hợp I là đường tròn ( C 1 ) đường kính AB nằm trong mặt phẳng (B, d).
Tương tự, tập hợp J là đường tròn ( C 2 ) đường kính AC nằm trong mặt phẳng (C, d) và tập hợp K là đường tròn đường kính AD nằm trong mặt phẳng (D, d).

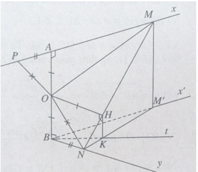
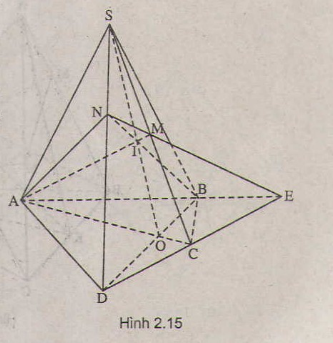
Theo giả thiết ta có M và N là hai điểm di động lần lượt trên hai tia Ax và By sao cho AM + BN = MN.
a) Kéo dài MA một đoạn AP = BN, ta có MP = MN và OP = ON.
Do đó ΔOMP = ΔOMN (c.c.c)
⇒ OA = OH nên OH = a.
Ta suy ra HM = AM và HN = BN.
b) Gọi M’ là hình chiếu vuông góc của điểm M trên mặt phẳng (Bx’, By) ta có:
HK // MM’ với K ∈ NM’.
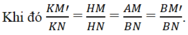
Do đó đối với tam giác BNM’ đường thẳng BK là phân giác của góc (x'By) .
c) Gọi (β) là mặt phẳng (AB, BK). Vì HK // AB nên HK nằm trong mặt phẳng (β) và do đó H thuộc mặt phẳng (β). Trong mặt phẳng (β) ta có OH = a. Vậy điểm H luôn luôn nằm trên đường tròn cố định, đường kính AB và nằm trong mặt phẳng cố định (β) = (AB, BK)

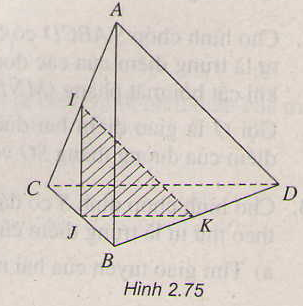
Dễ thấy P là điểm chính giữa \widebatEF\widebatEF nên D,N,P thẳng hàng
Cần chứng minh ˆIMC=ˆPDCIMC^=PDC^
Ta có : ˆIMC=ˆMIB+ˆB1=12ˆBIC+ˆB1=12(180o−ˆB1−ˆC1)+ˆB1IMC^=MIB^+B1^=12BIC^+B1^=12(180o−B1^−C1^)+B1^
=12(180o−ˆABC2−ˆACB2)+ˆABC2=90o+ˆABC4−ˆACB4=12(180o−ABC^2−ACB^2)+ABC^2=90o+ABC^4−ACB^4
ˆPDC=ˆPDE+ˆEDC=12ˆEDF+ˆEDCPDC^=PDE^+EDC^=12EDF^+EDC^=12(180o−ˆFDB−ˆEDC)+ˆEDC=12(180o−FDB^−EDC^)+EDC^
=90o−ˆFDB2+ˆEDC2=90o−90o−ˆB12+90o−ˆC12=90o−FDB^2+EDC^2=90o−90o−B1^2+90o−C1^2
=90o+ˆABC4−ˆACB4=90o+ABC^4−ACB^4
⇒ˆIMC=ˆPDC⇒IM//ND⇒IMC^=PDC^⇒IM//ND
b) Theo câu a suy ra ˆMID=ˆIDPMID^=IDP^
Mà ΔPIDΔPIDcân tại I ( do IP = ID ) nên ˆIPD=ˆIDPIPD^=IDP^
Suy ra ˆMID=ˆIPD=ˆQPNMID^=IPD^=QPN^
⇒ΔIDM≈ΔPQN(g.g)⇒ΔIDM≈ΔPQN(g.g)
c) từ câu b ⇒IMPN=IDPQ=IPPQ⇒IMPN=IDPQ=IPPQ( 1 )
Theo hệ thức lượng, ta có : IQ.IA=IE2=IP2IQ.IA=IE2=IP2
Do đó : QPIP=1−IQIP=1−IPIA=PAIAQPIP=1−IQIP=1−IPIA=PAIA
Suy ra IPQP=IAPAIPQP=IAPA( 2 )
Từ ( 1 ) và ( 2 ) ⇒IMPN=IAPA⇒IMPN=IAPAkết hợp với IM // PN suy ra A,M,N thẳng hàng

Câu 1:
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
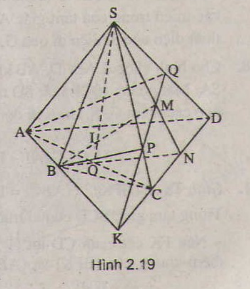
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy


Gọi (C) là đường tròn tâm O bán kính r, \(\left(C_1\right)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng qua tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \(\left(C_1\right)\).
Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') và \(\left(C_1\right)\).

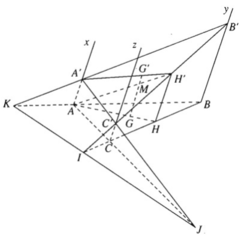
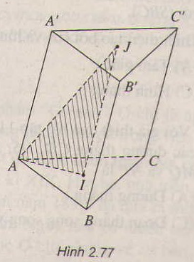
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
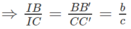
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
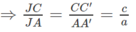
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
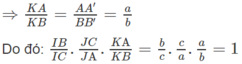
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
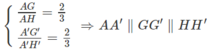
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
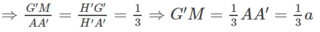
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
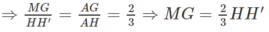
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
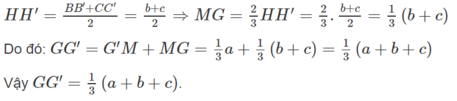



Cho a,b,c > 0 chứng minh rằng:
1 a+b+\(\dfrac{1}{4}\)≥ \(\sqrt{a+b}\)
2. (a+b+\(\dfrac{1}{4}\))^2+(b+c+\(\dfrac{1}{4}\))^2+(c+a+\(\dfrac{1}{4}\))^2 ≥ (\(\dfrac{1}{\dfrac{1}{a}+\dfrac{1}{b}}\)+\(\dfrac{1}{\dfrac{1}{b}+\dfrac{1}{c}}\)+\(\dfrac{1}{\dfrac{1}{c}+\dfrac{1}{a}}\))
Giúp mk với!!