Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc ADB=1/2*180=90 độ
góc ANB=góc ADB=90 độ
Xét ΔEAB có
BD,AN,EC là đường cao
BD cắt EC tại F
=>F là trựctâm
góc ADF+góc ACF=180 độ
=>ADFC nội tiếp
góc EDF+góc ENF=180 độ
=>EDFN nội tiếp
góc CDF=góc CAF
góc NDF=góc ECB
mà góc CAF=góc ECB
nên góc CDF=góc NDF
=>DF là phân giác của góc NDC(1)
góc DNF=góc AEC
góc CNF=góc DBA
góc AEC=góc DBA
=>góc DNF=góc CNF
=>NF là phân giác của góc DNC(2)
Từ (1), (2) suy ra F là tâm đường tròn nội tiêp ΔCND

a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)
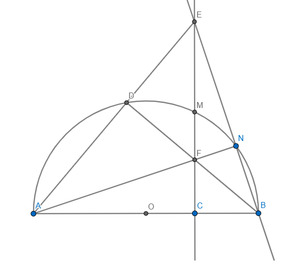

a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

1) Vì AB là đường kính \(\Rightarrow\angle ADB=90\) mà \(\angle ECB=90\Rightarrow BCDE\) nội tiếp
2) Vì \(\left\{{}\begin{matrix}EF\bot AB\\AF\bot EB\end{matrix}\right.\Rightarrow F\) là trực tâm tam giác EAB \(\Rightarrow BF\bot AE\)
mà \(BD\bot AE\left(\angle BDA=90\right)\Rightarrow B,F,D\) thẳng hàng
Ta có: \(\angle FNB+\angle FCB=90+90=180\Rightarrow FNBC\) nội tiếp
Xét \(\Delta AFC\) và \(\Delta ABN:\) Ta có: \(\left\{{}\begin{matrix}\angle ACF=\angle ANB=90\\\angle NABchung\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta ABN\left(g-g\right)\Rightarrow\dfrac{AF}{AC}=\dfrac{AB}{AN}\Rightarrow AF.AN=AB.AC\)
Tương tự \(\Rightarrow BF.BD=BC.BA\)
\(\Rightarrow AF.AN+BF.BD=AB.AC+AB.BC=AB^2=4R^2\)
3) Gọi G là giao điểm của (AEF) và AB
Ta có: \(\angle FGB=\angle AEF\left(AEFGnt\right)=\angle DBA\left(BCDEnt\right)\Rightarrow\Delta GFB\) cân tại F có \(FC\bot GB\Rightarrow CB=CG\)
mà C,B cố định \(\Rightarrow G\) cố định
Vì AEFG nội tiếp \(\Rightarrow I\in\) trung trực AG mà A,G cố định \(\Rightarrow\) đpcm

1: Ta có \(\widehat{CDE}=\widehat{CNE}=90^o\) nên tứ giác CDNE nội tiếp đường tròn đường kính CE.
2: Xét tam giác \(BKD\) và tam giác \(EKM\) có: \(\widehat{BKD}=\widehat{EKM}\) (đối đỉnh), \(\widehat{BDK}=\widehat{EMK}\) (= \(90^o\))
Do đó \(\Delta BKD\sim\Delta EKM(g.g)\).
Suy ra \(\dfrac{KB}{KD}=\dfrac{KE}{KM}\Rightarrow KB.KM=KE.KD\).
Do K là trực tâm của tam giác BCE nên C, K, N thẳng hàng.
3: Ta có \(\widehat{FNK}=\dfrac{1}{2}sđ\stackrel\frown{NC}=\widehat{NBC}=90^o-\widehat{BED}=\widehat{NKF}\). Suy ra tam giác NKF cân tại F nên FN = FK. Lại có tam giác ENK vuông tại N nên F là trung điểm của EK.
Vậy ta có đpcm.

B C O A D d M K E N I H F P d'
1) Xét nửa đường tròn (O) đường kính BC có điểm N thuộc (O) => ^CNB = 900
=> ^CNE = 1800 - ^CNB = 900. Xét tứ giác CDNE có:
^CDE = ^CNE = 900 => Tứ giác CDNE nội tiếp đường tròn (đpcm).
2) Ta có điểm M thuộc nửa đường tròn (O) đường kính BC => ^CMB = 900
=> BM vuông góc CE. Xét \(\Delta\)BEC:
BM vuông góc CE; ED vuông góc BC; BM giao ED tại K => K là trực tâm \(\Delta\)BEC
=> CK vuông góc BE. Mà CN vuông góc BE (Do ^CNB = 900) => 3 điểm C;K;N thẳng hàng (đpcm).
3) Gọi giao điểm của MN với DE là H. Lấy F là trung điểm của EH. BH cắt CF tại điểm P.
Xét tứ giác CMHD: ^CMH = ^CDH = 900 => CMKD nội tiếp đường tròn => ^MCK = ^MDK (1)
Tương tự: ^NBK = ^NDK (2)
Từ (1) & (2) => ^MDK = ^NDK hay ^MDH = ^FDN
Tương tự: ^DMB = ^NMB => ^DMH = 2.^DMB (3)
Dễ thấy tứ giác BDME nội tiếp đường tròn => ^DMB = ^BED (2 góc nt chắn cung BD)
Hay ^DMB = ^NEF. Xét \(\Delta\)ENH vuông tại N: H là trung điểm EH
=> \(\Delta\)NEF cân tại F. Do ^DFN là góc ngoài \(\Delta\)NEF => ^DFN = 2.^NEF
Mà ^DMB = ^NEF (cmt) => ^DFN = 2.^DMB (4)
Từ (3) & (4) => ^DMH = ^DFN. Xét \(\Delta\)DMH và \(\Delta\)DFN:
^DMH = ^DFN ; ^MDH = ^FDN (cmt) => \(\Delta\)DMH ~ \(\Delta\)DFN (g.g)
=> \(\frac{DM}{DF}=\frac{DH}{DN}\)=> \(DH.DF=DM.DN\)(5)
Dễ chứng minh \(\Delta\)CMD ~ \(\Delta\)NBD => \(\frac{DM}{DB}=\frac{DC}{DN}\Rightarrow DM.DN=DB.DC\)(6)
Từ (5) & (6) => \(DH.DF=DB.DC\)\(\Rightarrow\frac{DH}{DB}=\frac{DC}{DF}\)
\(\Rightarrow\Delta\)CDH ~ \(\Delta\)FDB (c.g.c) => ^DHC = ^DBF. Mà ^DHC + ^DCH = 900
=> ^DBF + ^DCH = 900 => CH vuông góc BF.
Xét \(\Delta\)CFB: FD vuông góc BC; CH vuôn góc BF; H thuộc FD => H là trực tâm \(\Delta\)CFB
=> BH vuông góc CF (tại P). Ta có nửa đg trong (O) đg kính BC và có ^CPB = 900
=> P thuộc nửa đường tròn (O) => Tứ giác CMPB nội tiếp (O)
=> ^BMP = ^BCP (2 góc nt chắn cung BP) Hay ^HMP = ^DCP
Xét tứ giác CPHD: ^CPH = ^CDH = 900 => ^DCP + ^DHP = 1800
=> ^HMP + ^DHP = 1800 hay ^HMP + ^KHP = 1800 => Tứ giác MPHK nội tiếp đg tròn
=> ^KMH = ^KPH (2 góc nt chắn cung KH) hay ^KMN = ^KPB.
Lại có tứ giác EMKN nội tiếp đg tròn => ^KMN = ^KEN => ^KMN = ^KEB
=> ^KPB = ^KEB => Tứ giác BKPE nội tiếp đg tròn. Mà 3 điểm B;K;E cùng thuộc (I)
=> Điểm P cũng thuộc đg tròn (I) => IP=IB => I thuộc trung trực của BP
Mặt khác: OP=OB => O cũng thuộc trung trực của BP => OI là trung trực của BP
=> OI vuông góc BP. Mà CF vuông góc BP (cmt) => OI // CF (7)
I nằm trên trung trực của EK và F là trung điểm EK => IF vuông góc EK => IF vuông góc d
OC vuông góc d => OC // IF (8)
Từ (7) & (8) => Tứ giác COIF là hình bình hành => IF = OC = R (bk của (O))
=> Độ dài của IF không đổi. Mà IF là khoảng cách từ I đến d (Do IF vuông góc d)
=> I nằm trên đường thẳng d' // d và cách d một khoảng bằng bán kính của nửa đường tròn (O)
Vậy điểm I luôn nằm trên d' cố định song song với d và cách d 1 khoảng = bk nửa đg tròn (O) khi M thay đổi.