Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

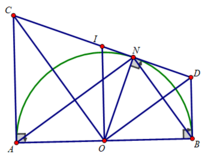
a)Ta có: DN và DB là hai tiếp tuyến cắt nhau tại D ⇒ DN = DB
CA và CN là hai tiếp tuyến cắt nhau tại C ⇒ CA = CN
Khi đó: DB + CA = DN + CN = DC
Mặt khác OC và OD lần lượt là hai phân giác của hai góc ∠(AON) và ∠(BON) kề bù nên
∠(COD) = 90 0
Trong tam giác vuông COD có ON là đường cao nên:
DN.CN = ON 2 = R 2
Hay AC.BD = R 2 (không đổi)

a: Xét (O) co
CM,CA là tiếp tuyên
=>CM=CA
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB
CD=CM+MD
=>CD=CA+BD
b: Xet ΔACN và ΔDBN có
góc NAC=góc NDB
góc ANC=góc DNB
=>ΔACN đồng dạng vơi ΔDBN
=>AC/BD=AN/DN
=>CN/MD=AN/ND
=>MN/AC

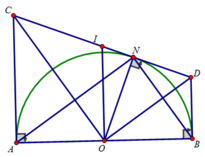
b) Gọi I là tâm của đường tròn đường kính CD.
Tứ giác CABD là hình thang vuông (AC ⊥ AB;BD ⊥ AB) có OI là đường trung bình
⇒ OI // AC ; mà AC ⊥ AB ⇒ OI ⊥ AB tại O
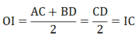
Vậy AB tiếp xúc với đường tròn đường kính CD.