Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

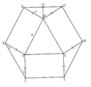
Số đo mỗi góc của ngũ giác đều là 1080.
Ta có tam giác ABC cân tại B
⇒ A 1 ^ = C 1 ^ = ( 180 0 − 108 0 ) : 2 = 36 0 ⇒ E A C ^ = D C A ^ (1)
Chứng minh tương tự ta được:
C 3 ^ = E ^ 1 = 36 0 ⇒ C 2 ^ = 36 0
Có C 2 ^ = E 1 ^ = 36 0 ⇒ E D / / A C (2)
Từ (1) và (2), suy ra ACDE là hình thang cân (ĐPCM)
(Các khác: Có thể chứng minh hình thang ACDE có hai đường chéo bằng nhau)
* Chứng minh tương tự ta có J E F ^ = E F G ^ = F G H ^ = G H I ^ = H I J ^ = I J E ^ .
Vậy tứ giác CDEK là hình bình hành
mà CD = DE, suy ra hình bình hành CDEK là hình thoi (ĐPCM)

Số đo mỗi góc của ngũ giác đều là $108^o$. Ta có $\Delta ABC$ cân tại $B$
$\Rightarrow \widehat{A_1}=\widehat{C_1}=(180^o-108^o):2=36^o$
$\Rightarrow \widehat{EAC}=\widehat{DCA}(1)$
Chứng minh tương tự ta được:
$\widehat{C_3}=\widehat{E_1}=36^o \Rightarrow \widehat{C_2}=36^o$
Có $\widehat{C_2}=\widehat{E_1}=36^o \Rightarrow ED//AC(2)$
Từ $(1)$ và $(2)$ suy ra $ACDE$ là hình thang cân.
Chứng minh tương tự ta có $\widehat{C_3}=\widehat{E_2}=36^o \Rightarrow EK//DC$
Vậy tứ giác $CDEK$ là hình bình hành
Mà $CD=DE$, suy ra hình bình hành $CDEK$ là hình thoi.

cj kham khảo
a) Nối AC; AD
Ngũ giác ABCDE được chia thành 3 tam giác: ΔABC, ΔACD, ΔADE. Tổng các góc trong của mỗi tam giác bằng 1800
Tổng các góc trong của ngũ giác ABCDE là 1800. 3 = 5400
b) Vì ABCDE là ngũ giác đều nên
\(\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=\widehat{E}=\frac{540^0}{5}=108^0\)
Mặt khác ΔABC cân tại B nên
\(\widehat{BAC}+\widehat{BCA}=\frac{180^0-108^0}{2}=36^0\)
\(\Rightarrow\widehat{CAE}=\widehat{ACD}=108^0-36^0=72^0\)
\(\Rightarrow\widehat{EDC}+\widehat{ADC}=108^0+72^2=180^0\)
Suy ra ED // AC hay ED // CF.
Chứng minh tương tự ta có EF // CD
Mặt khác ED = DC (gt)
nên tứ giác CEFD là hình thoi.

Bài 2:
a: Xet ΔABC có AD/AB=AF/AC
nen DF//BC và DF=1/2BC
=>BDFC là hình thang
mà góc B=góc C
nên BDFC là hình thang cân
b Xet ΔABC có
CE/CB=CF/CA
nên EF//AB và EF=AB/2
=>EF//AD và EF=AD
=>ADEF là hình bình hành
mà AD=AF
nen ADEF là hình thoi
c: Để ADEF là hình vuông thì góc BAC=90 độ

a) Tứ giác BHCkBHCk có 2 đường chéo BCBC và HKHK cắt nhau tại trung điểm MM của mỗi đường
⇒BHCK⇒BHCK là hình bình hành.
b) BHCKBHCK là hình bình hành ⇒BK∥HC⇒BK∥HC
Mà HC⊥ABHC⊥AB
⇒BK⊥AB⇒BK⊥AB (đpcm)
c) Do II đối xứng với HH qua BC⇒IH⊥BCBC⇒IH⊥BC mà HD⊥BC,D∈BCHD⊥BC,D∈BC
⇒I⇒I đối xứng với HH qua D⇒DD⇒D là trung điểm của HIHI
Và MM là trung điểm của HKHK
⇒DM⇒DM là đường trung bình ΔHIKΔHIK
⇒DM∥IK⇒DM∥IK
⇒BC∥IK⇒BC∥IK
⇒BCKI⇒BCKI là hình thang
ΔCHIΔCHI có CDCD vừa là đường cao vừa là đường trung tuyến
⇒ΔCHI⇒ΔCHI cân đỉnh CC
⇒CI=CH⇒CI=CH (*)
Mà tứ giác BHCKBHCK là hình bình hành ⇒CH=BK⇒CH=BK (**)
Từ (*) và (**) suy ra CI=BKCI=BK
Tứ giác BCKIBCKI là hình bình hành có 2 đường chéo CI=BKCI=BK
Suy ra BCIKBCIK là hình thang cân.
Tứ giác HGKCHGKC có GK∥HCGK∥HC (do BHCKBHCK là hình bình hành)
⇒HGKC⇒HGKC là hình thang có đáy là GK∥HCGK∥HC
...

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
b: Xét ΔABC có
H là trung điểm của BC
N là trung điểm của AC
DO đó: HN là đường trung bình
=>HN//AB và HN=AB/2
=>HN=AM và HN=AM
Xét tứ giác AMHN có
HN//AM
HN=AM
Do đó: AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi
c: Ta có: AMHN là hình thoi
nên Hai đường chéo AH và MN cắt nhau tại trung điểm của mỗi đường
=>O là trung điểm của AH
Xét tứ giác ABHK có
HK//AB
HK=AB
DO đó: ABHK là hình bình hành
Suy ra: Hai đường chéo AH và BK cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AH
nên O là trung điểm của BK
a: góc BAE=góc BCD=góc ABC=góc AED=góc CDE=108 độ
góc BAC=góc BCA=(180-108)/2=36 độ
=>góc CAE=góc ACD=72 độ
Vì góc CAE+góc AED=180 độ
nên AC//ED
mà góc AED=góc CDE
nên ACDE là hình thang cân
b: góc ABE=góc AEB=(180-108)/2=36 độ
góc AKE=180 độ-72 độ-36 độ=72 độ=góc ACD
=>KE//DC
Xet tứ giác KCDE có
KC//DE
KE//CD
KC=CD
DO đó: KCDE là hình thoi