Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta gọi số tự nhiên sau khi thêm 5 vào bên phải là: xyz5; x,y,z là các chữ số chưa biết của số tự nhiên đó.
Ta có: xỵz5 - xyz = 1796
Để tìm được số tự nhiên xyz ta phải xét từng cặp số.
Cặp I: là 5 và z
5-z=6 không được nên phải mượn 1 tức là 15 - z = 6 => z=9
Cặp II: z - y = 9 - y = 9 bởi vì cặp I là 5 mượn một nên bây giờ phải trả: 9 - y - 1= 9 = 8-y=9; 8 - y không thể bằng 9 nên ta phải mượn 1 là 18 - y = 9=> y=9
Tiếp theo y - x = 9 - x = 7 , cặp 2 mượn 1 nên giờ phải trả : 9 - x - 1= 7 => x = 1
Thế là ta đã tìm được số tự nhiên xyz= 199
Thử lại nhé:
199 viết thêm số 5 bân phải là 1995
1995 - 199 = 1796
Vậy là đúng rồi
theo đó ta có sơ đồ : _ abc5
1796
abc tính dễ lắm .khi 5-6=9 thì c = 9.ta lại lấy 9-9=b.rồi lại lấy b-7 .....rồi cứ tiếp tục như vậy
tinh ra thì ta được abc =199

Số viết thêm là :
2004 : ( 10 - 1 ) = 222 ( dư 6 )
Vậy số viết thêm là 6
Số viết thêm là :
2004 : ( 10-1 ) = 222 dư 6
Vậy số viết thêm là 6

ta có : 2013/(10-1)=223[dư 6]
vậy số đã cho là 223 . chữ số viết thêm là 6

Cách 1 : Khi viết thêm một chữ số nào đó vào bên phải một số tự nhiên đã cho ta được số mới bằng 10 lần số tự nhiên đó cộng thêm chính chữ số viết thêm. Gọi chữ số viết thêm là a, ta có sơ đồ
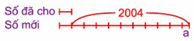
9 lần số đã cho là : 2004 - a.
Số đã cho là : (2004 - a) : 9.
Vì số đã cho là số tự nhiên nên 2004 - a phải chia hết cho 9, số 2004 chia 9 dư 6 nên a chia cho 9 phải dư 6, mà a là chữ số nên a = 6. Số tự nhiên đã cho là (2004 - 6) : 9 = 222.
Cách 2 : Gọi số tự nhiên đã cho là A chữ số viết thêm là x thì số mới là A x ¯ .
Ta có A x ¯ - A = 2004
A x 10 + x - A = 2004 (phân tích số)
A x 10 - A + x = 2004
A x (10 - 1) + x = 2004 (một số nhân với một tổng)
A x 9 + x = 2004
Vì A x 9 chia hết cho 9 ; 2004 chia 9 dư 6 nên x chia cho 9 phải dư 6. Vì x là chữ số nên x = 6. Ta có :
A x 9 + 6 = 2004
A x 9 = 2004 - 6
A x 9 = 1998
A = 1998 : 9
A = 222.
Vậy số tự nhiên đã cho là 222 ; chữ số viết thêm là 6.

Giả sử chữ số được viết thêm vào bên phải số đã cho là chữ số \(a\), khi đó số mới bằng \(10\)lần số đã cho cộng thêm \(a\)đơn vị.
Hiệu của số mới và số đã cho là \(9\)lần số đã cho và \(a\)đơn vị.
Có \(2011=9\times223+4\)chia cho \(9\)dư \(4\)nên chữ số \(a\)là chữ số \(4\).
Số phải tìm là:
\(\left(2011-4\right)\div9=223\)

gọi số ban đầu là x, chữ số thêm vào là y
khi đó ta có số mới có giá trị là \(10\times x+y\)
ta có :\(10\times x+y-x=2004\)
hay \(9\times x+y=2004\text{ hay }9x=2004-y\)
nên \(11139-y\text{ chia hết cho 9}\) mà y là chữ số nên \(0\le y\le9\)
\(\Rightarrow y=6\)
vậy số thêm vào là 6