Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(BM=2MA\Rightarrow\overrightarrow{AM}=\dfrac{1}{3}\overrightarrow{AB}\); \(AN=3NC\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\)
Do đó:
\(\overrightarrow{MN}.\overrightarrow{DN}=\left(\overrightarrow{MA}+\overrightarrow{AN}\right)\left(\overrightarrow{DA}+\overrightarrow{AN}\right)\)
\(=\left(-\dfrac{1}{3}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\left(-\overrightarrow{AD}+\dfrac{3}{4}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\)
\(=\left(\dfrac{5}{12}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AD}\right)\left(\dfrac{3}{4}\overrightarrow{AB}-\dfrac{1}{4}\overrightarrow{AD}\right)\)
\(=\dfrac{5}{16}AB^2-\dfrac{3}{16}AD^2=\dfrac{1}{8}AB^2=\dfrac{1}{8}\) (chú ý rằng \(\overrightarrow{AB}.\overrightarrow{AD}=0\) và \(AB=AD=1\))

A B C D O M N
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).

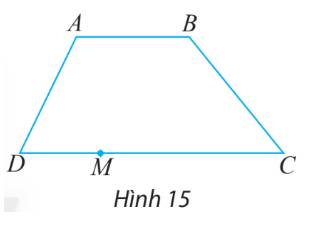
a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)

BM=BC/2=10cm
\(AM=\sqrt{20^2+10^2}=10\sqrt{5}\left(cm\right)\)
Xét ΔABM vuông tại B có sin BAM=BM/AM=10/10căn 5
nên cos BAM=2/căn 5
\(\overrightarrow{AB}\cdot\overrightarrow{AM}=AB\cdot AM\cdot cosBAM=20\cdot10\sqrt{5}\cdot\dfrac{2}{\sqrt{5}}\)
\(=20\cdot10\cdot2=40\cdot10=400\)