Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ phương trình chính tắc của (E) ta có: \(a = 7,b = 5 \Rightarrow c = 2\sqrt 6 {\rm{ }}(do{\rm{ }}{{\rm{c}}^2} + {b^2} = {a^2})\)
Vậy ta có tọa độ các giao điểm của (E) với trục Ox, Oy là: \({A_1}\left( { - 7;{\rm{ }}0} \right)\)\({A_2}\left( {7;{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ 5}}} \right)\)\({B_2}\left( {0;{\rm{ 5}}} \right)\)
Hai tiêu điểm của (E) có tọa độ là: \({F_1}\left( { - 2\sqrt 6 ;0} \right),{F_2}\left( {2\sqrt 6 ;0} \right)\)

Tiêu cự là \(2c\), độ dài trục lớn là \(2a\) \(\Rightarrow\dfrac{2c}{2a}=\dfrac{1}{2}\Rightarrow a=2c\) (1)
Phương trình elip có dạng:
\(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\Leftrightarrow\dfrac{x^2}{a^2}+\dfrac{y^2}{a^2-c^2}=1\) (2)
Thay (1) vào (2):
\(\Leftrightarrow\dfrac{x^2}{4c^2}+\dfrac{y^2}{3c^2}=1\) (3)
Do elip qua A, thay tọa độ A vào (3):
\(\Rightarrow\dfrac{6^2}{4c^2}+\dfrac{0}{3c^2}=1\Rightarrow c=3\) \(\Rightarrow a=2c=6\)
\(\Rightarrow b^2=a^2-c^2=27\)
Vậy pt elip là: \(\dfrac{x^2}{36}+\dfrac{y^2}{27}=1\)

Do (E) giao với Ox tại \({A_1}\left( { - 5;0} \right)\) nên ta có: \(a = 5\)
Do (E) giao với Oy tại \({B_2}\left( {0;\sqrt {10} } \right)\) nên ta có: \(b = \sqrt {10} \)
Vậy phương trình chính tắc của (E) là: \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{10}} = 1\)

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
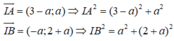
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
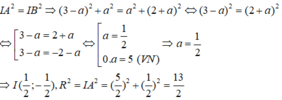
Vậy phương trình đường tròn có dạng:
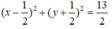
Ta có:
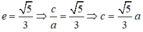
Giả sử elip (E) có dạng:
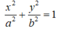
Vì (E) đi qua B nên:
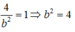
Mà
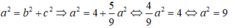
Vậy phương trình chính tắc của elip (E) là:
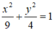

Gọi phương trình chính tắc elip cần tìm là
![]() .
.
Do elip đi qua
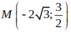 ,
, 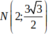
nên ta có hệ
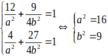
Vậy elip cần tìm là
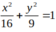
Chọn C.

