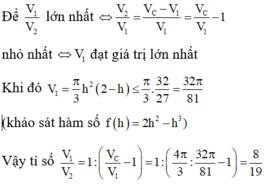
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
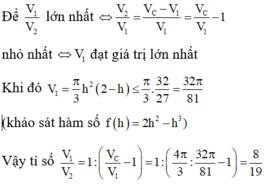
Chọn C
Lời giải.
Ta có
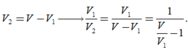
Suy ra V 1 V 2 lớn nhất khi V V 1 nhỏ nhất => V 1 đạt giá trị lớn nhất.
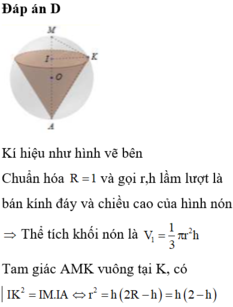
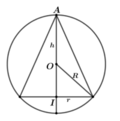
Gọi h,r lần lượt là chiều cao và bán kính đáy của hình nón nội tiếp mặt cầu.
Gọi I, O lần lượt là tâm của đường tròn đáy hình nón và tâm của mặt cầu.
Gọi A là đỉnh của hình nón. Xét thiết diện qua trục của hình nón như hình vẽ bên.
Xét hàm
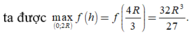
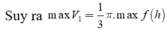
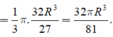
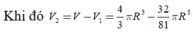
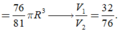
Cách 2.
TH1. Chiều cao của khối nón h= R + x và bán kính đáy r 2 = R 2 - x 2
Theo BĐT Cô si cho 3 số dương, ta có
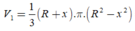
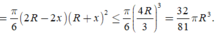
Dấu "=" xảy ra
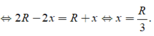
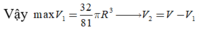
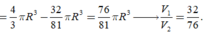
TH2. Chiều cao của khối nón h = R - x. Làm tương tự.
2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)
