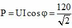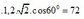Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

Điện áp giữ hai đầu đoạn mạch lệch pha \(\frac{\pi}{3}\) so với cường độ dòng điện:
\(\Rightarrow\cos\left(\frac{\pi}{3}\right)=\frac{R}{Z}\Leftrightarrow Z=80\Omega\)

tan \(\varphi\)=1=\(\frac{Z_C-Z_L}{R}\Rightarrow\)ZC=R+\(\omega\)L=125
CHỌN A
Cho mình hỏi là sao phi lại bằng 1 vậy. Giải thích mình tí với

Ta lấy \(U_R=1\)
\(\Rightarrow U_L=2\), \(U_C=1\)
\(\tan\varphi=\frac{U_L-U_C}{U_R}=\frac{2-1}{1}=1\)
\(\Rightarrow\varphi=\frac{\pi}{4}\)
Vậy u sớm pha hơn i là \(\frac{\pi}{4}\), hay i trễ pha với u là \(\frac{\pi}{4}\)

\(Z_L=Z\omega=L.2\pi f_1\rightarrow L=\frac{36}{2\pi f_1}\)
\(Z_C=\frac{1}{C.2\pi f_1}\rightarrow C=\frac{1}{144.2\pi.f_1}\)
khi \(f=f_2\) cường độ dòng điện cùng pha với hiệu điện thế tức là xảy ra cộng hưởng
\(\omega^2_2=\frac{1}{LC}\Leftrightarrow\frac{36}{144.f^2_1}=\frac{1}{120^2}\rightarrow f_1=60Hz\)

Áp dụng: \(P=\dfrac{U^2}{R}\cos^2\varphi\)
\(\Rightarrow 160=\dfrac{U^2}{R}.0,4^2\) (1)
\(340=\dfrac{U^2}{R}.\cos^2\varphi\) (2)
Lấy (1) chia (2) vế với vế ta tìm đc \(\cos\varphi = 0,6\)
\(P_1=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_1\)
\(P_2=UI.cos\varphi=\frac{U^2.R}{Z.R}.cos\varphi=\frac{U^2}{R}.cos\varphi^2_2\)
\(cos\varphi_2=0,6\)
đáp án B

\(U_{RC}=const=U\) khi \(Z_{L1}=2Z_C=R\)
Mặt khác L thay đổi để : \(U_{Lmax}:U_{Lmax}=\frac{U\sqrt{R^2+Z^2_C}}{R}=\frac{U\sqrt{2^2+1}}{2}=\frac{U\sqrt{5}}{2}\)
\(\Rightarrow chọn.D\)
+,có C=C1=>U_R=\frac{U.R}{\sqrt{R^2+(Zl-ZC1)^2}}
+,U R ko đổi =>Zl=ZC1
+,có c=C1/2=>ZC=2ZC1
=>U(AN)=U(RL)=\frac{U\sqrt{r^2+Z^2l}}{\sqrt{R^2+(Zl-2Z^2C1)}}=u=200V
Đáp án B
+ Ta có: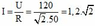 A.
A.
+ Công suất tỏa nhiệt của mạch là: