Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

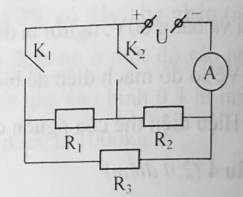
a)Khóa \(K_1\) đóng, khóa \(K_2\) mở ta có CTM: \(\left(R_1ntR_2\right)//R_3\)
\(I_A=I_m=1A\)
\(R_{12}=R_1+R_2=5+5=10\Omega\)
\(R_{tđ}=\dfrac{R_{12}\cdot R_3}{R_{12}+R_3}=\dfrac{10\cdot15}{10+15}=6\Omega\)
\(U=R_{tđ}\cdot I=6\cdot1=6V=U_{12}=U_3\)
\(I_1=I_2=I_{12}=\dfrac{U_{12}}{R_{12}}=\dfrac{6}{10}=0,6A\)
\(I_3=1-0,6=0,4A\)
b)Khóa \(K_1\) mở và khóa \(K_2\) đóng ta có CTM: \(R_2//\left(R_1ntR_3\right)\)
\(R_{13}=R_1+R_3=5+15=20\Omega\)
\(R_{tđ}=\dfrac{R_2\cdot R_{13}}{R_2+R_{13}}=\dfrac{5\cdot20}{5+20}=4\Omega\)
\(I_A=\dfrac{U}{R_{tđ}}=\dfrac{6}{4}=1,5A\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{U}{R_2}=\dfrac{6}{15}=0,4A\)
\(I_1=I_3=I_{13}=I-I_2=1,5-0,4=1,1A\)

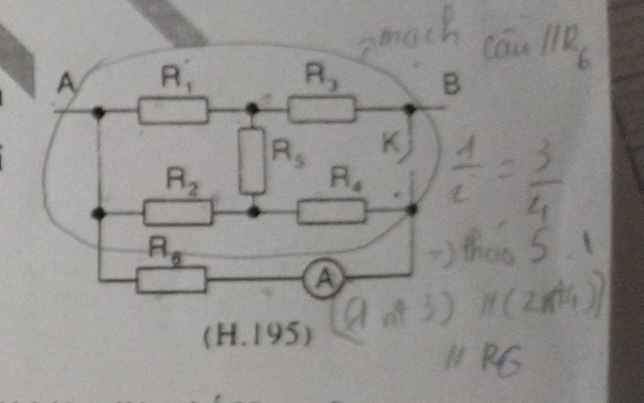
ta thấy \(\dfrac{R_1}{R_2}=\dfrac{R_3}{R_4}=2\) => mạch cầu cân bằng => I5=0 U5=0
khi K đóng \(R_{1234}=\dfrac{\left(R_1+R_3\right)\left(R_2+R_4\right)}{R_1+R_2+R_3+R_4}=4\left(\Omega\right)\)
\(R_{td}=\dfrac{R_6.R_{1234}}{R_6+R_{1234}}\)
\(\Rightarrow I_A=I=\dfrac{U_{AB}}{R_{td}}=\dfrac{48}{2}=24\left(A\right)\)
em đang ôn hsg lí 9 à :???

* th1: khi K đóng\(=>R1//\left[R2nt(Rđ//R3)\right]\)
\(=>U=U\left(23đ\right)=U1=90V\)
\(=>I1=\dfrac{U1}{R1}=\dfrac{90}{45}=2\left(A\right)\)
\(=>R\left(3đ\right)=\dfrac{R3.Rđ}{R3+Rđ}=\dfrac{45Rđ}{45+Rđ}\)
\(=>I\left(đ\right)=\dfrac{U3}{Rđ}=\dfrac{R3.I\left(23đ\right)}{Rđ}=\dfrac{45}{Rđ}.I\left(23đ\right)\)
\(=\dfrac{45}{Rđ}.\dfrac{U}{R\left(23đ\right)}=\dfrac{45}{Rđ}.\dfrac{90}{R2+\dfrac{R3.Rđ}{R3+Rđ}}=\dfrac{45}{Rđ}.\dfrac{90}{90+\dfrac{45Rđ}{45+Rđ}}\left(1\right)\)
Th2:: khi K mở\(=>R3nt\left[R2//\left(R1ntRđ\right)\right]\)
\(=>Rtd=\dfrac{\left(R1+Rđ\right)R2}{R1+R2+Rđ}+R3=\dfrac{\left(45+Rđ\right)90}{135+Rđ}+45\)
\(=\dfrac{4050+6075+90Rđ+45Rđ}{135+Rđ}=\dfrac{10125+135Rđ}{135+Rđ}\left(om\right)\)
\(=>I\left(đ\right)=Im-I2=\dfrac{U}{Rtđ}-\dfrac{U2}{R2}\)
\(=\dfrac{90\left(135+Rđ\right)}{10125+135Rđ}-\dfrac{90-U3}{90}\)
\(=\dfrac{90\left(135+Rđ\right)}{10125+135Rđ}-1+\dfrac{Im.R3}{90}\)
\(=\dfrac{90\left(135+Rđ\right)}{10125+135Rđ}-1+\dfrac{\dfrac{90.45\left(135+Rđ\right)}{10125+135Rđ}}{90}\left(2\right)\)
(1)(2)
\(=>\dfrac{90\left(135+Rđ\right)}{10125+135Rđ}-1+\dfrac{\dfrac{90.45\left(135+Rđ\right)}{10125+135Rđ}}{90}=\dfrac{45.90}{Rđ.\left(90+\dfrac{45Rđ}{45+Rđ}\right)}\)
\(=>Rđ=95,4\left(om\right)\)
trong tính toán có thể bị sai sót nên mong bạn kiểm tra cho kĩ, cách làm như vậy

cái bài này nãy tui làm rồi nhưng mà hơi sai sót
bạn có thể đặt Rđ=x(ôm) rồi từ đó
tính I(đ) theo mạch điện trong 2 trươngf hợp K đóng, K mở
(có ẩn x)
mà cường độ dòng điện định mức đèn như nhau trong cả 2 trường hợp
thì bạn suy ra được I(đ) trong TH1 = I(đ) trong TH2
(có ẩn x) rồi giải pt=>x=Rđ=15(ôm)
(bài này hơi dài nên tui gợi ý thế bn tự làm nhé)

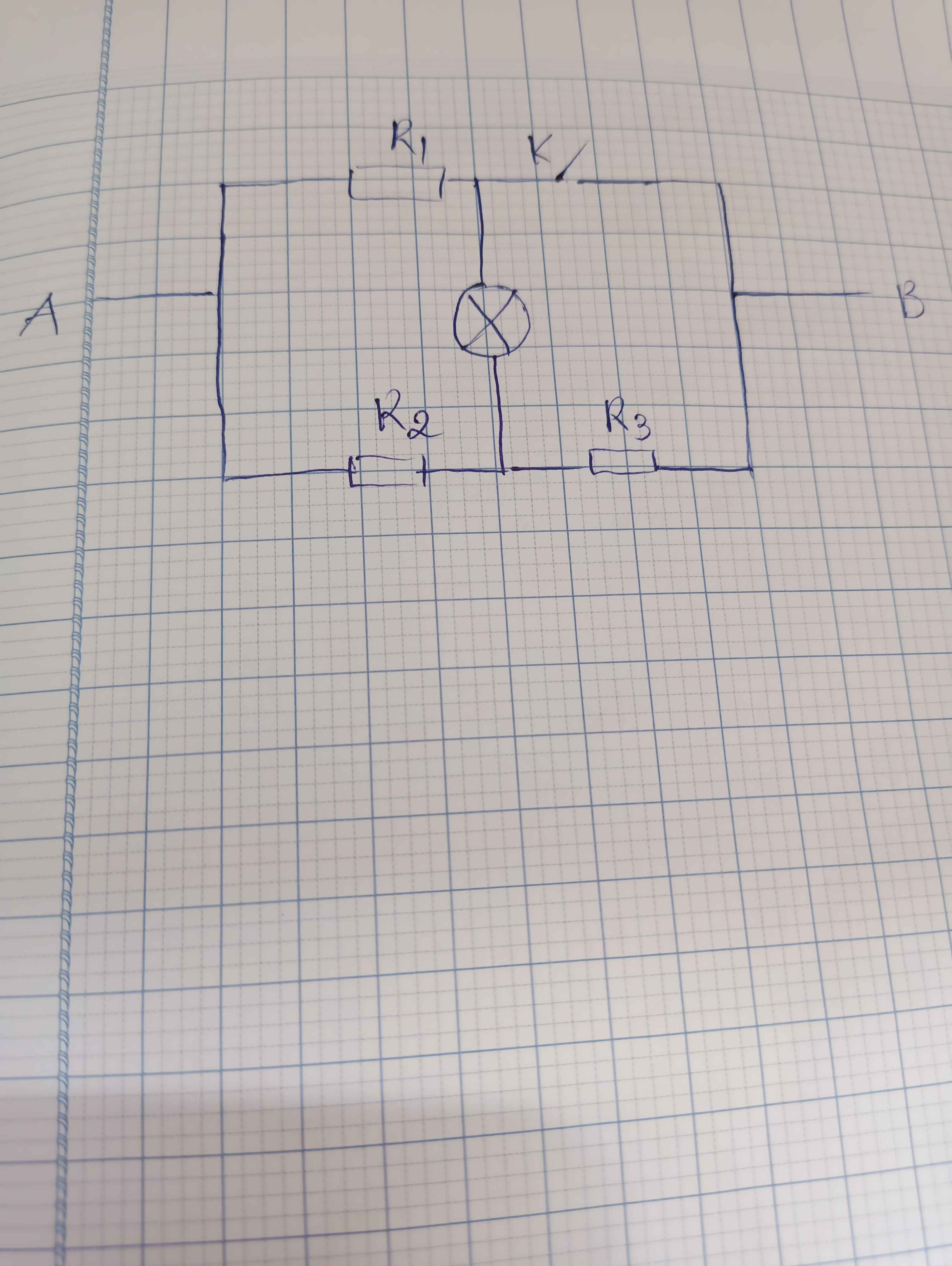 Cho mạch điện như hình. R1=R3=45 ôm R2=90 ôm D là 1 bóng đèn khoá K có điện trở không đáng kể Hiệu Điện thế U ko thay đổi=90V biết rằng khi k ngắt hoặc k đóng đèn đều sáng bthuong hãy tính điện trở và hiệu điện thế định mức của đèn
Cho mạch điện như hình. R1=R3=45 ôm R2=90 ôm D là 1 bóng đèn khoá K có điện trở không đáng kể Hiệu Điện thế U ko thay đổi=90V biết rằng khi k ngắt hoặc k đóng đèn đều sáng bthuong hãy tính điện trở và hiệu điện thế định mức của đèn
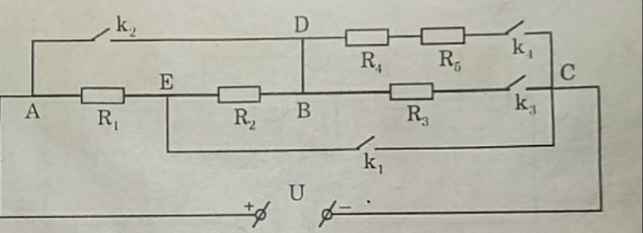
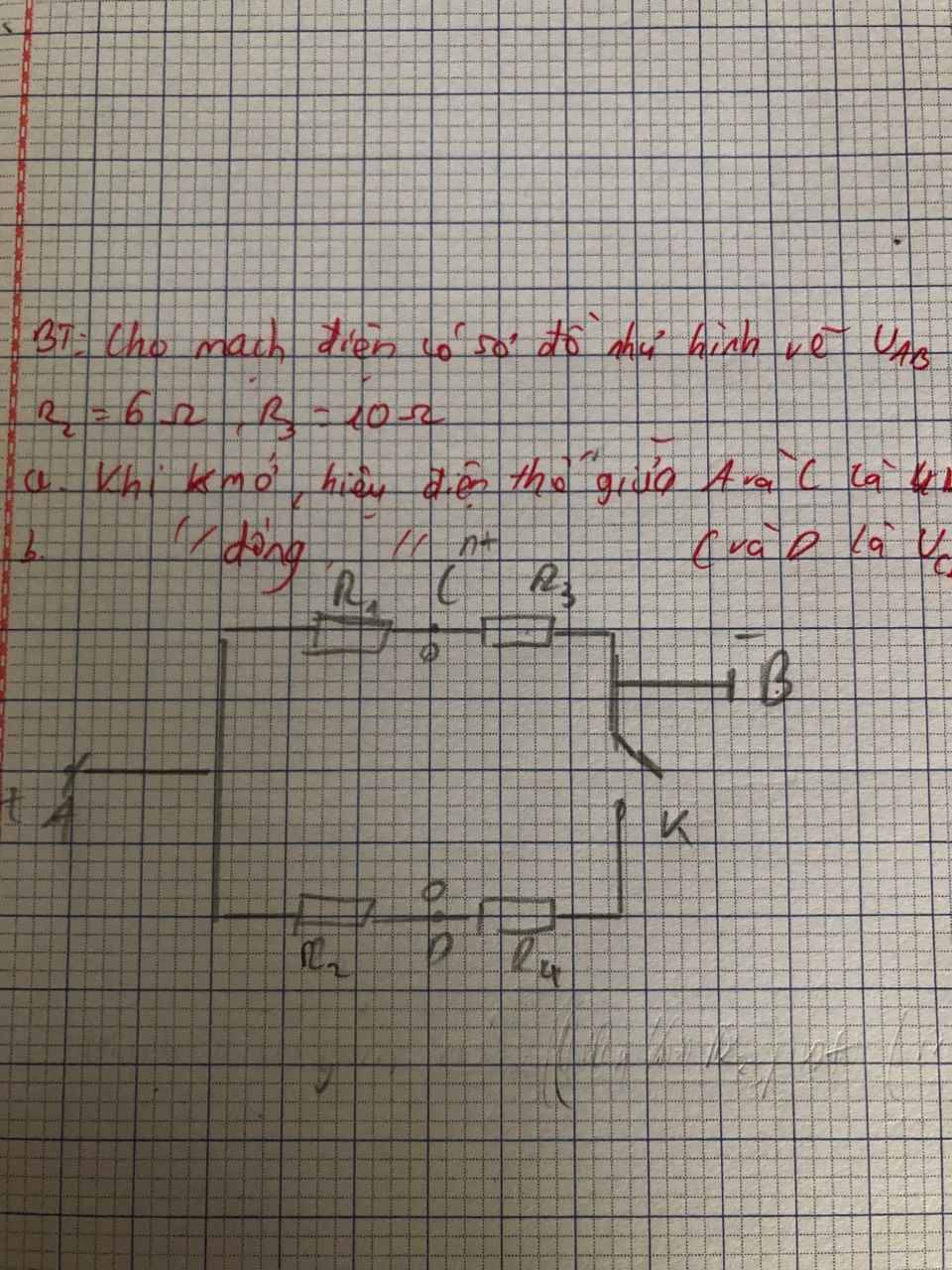
a.
K mở thì không có dòng điện chạy qua \(R_2\Rightarrow U_{DC}=U_{AC}=2V\)
Ta có: \(R_1ntR_3\Rightarrow R_{td}=R_1+R_3=R_1+5\left(\Omega\right)\)
\(I=I_{AC}\Leftrightarrow\dfrac{U}{R_{td}}=\dfrac{U_{AC}}{R_1}\Leftrightarrow\dfrac{2}{R_1}=\dfrac{12}{R_1+5}\)
\(\Rightarrow12R_1=2R_1+10\)
\(\Leftrightarrow6R_1=R_1+5\)
\(\Leftrightarrow R_1=1\Omega\)
b.
K đóng thì thì mạch có dạng: \(\left(R_1ntR_3\right)//\left(R_2ntR_4\right)\)
Ta có: \(\left\{{}\begin{matrix}R_{13}=R_1+R_3=1+5=6\Omega\\U_{13}=U_{24}=U=12V\\I_{13}=\dfrac{U_{13}}{R_{13}}=\dfrac{12}{6}=2A\end{matrix}\right.\) \(\Rightarrow U_{AC}=2\cdot1=2V\)
\(\Rightarrow U_{CD}=U_{AD}-U_{AC}=U_{AD}-2\)
\(\Rightarrow U_{AD}=2+U_{CD}=2+1=3V\)
Ta có: \(\left\{{}\begin{matrix}I_{24}=\dfrac{U}{R_{24}+3}=\dfrac{12}{R_{24}+3}\\I_2=\dfrac{U_{AD}}{R_2}=1\end{matrix}\right.\)
Do \(\left(R_2ntR_4\right)\Rightarrow\dfrac{12}{R_{24}+3}=1\Rightarrow R_4=9\Omega\)