Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bài này hơi dài nên bạn chỉ cần tính theo mạch phân tích từng ý(cơ bản sẽ ra thôi)
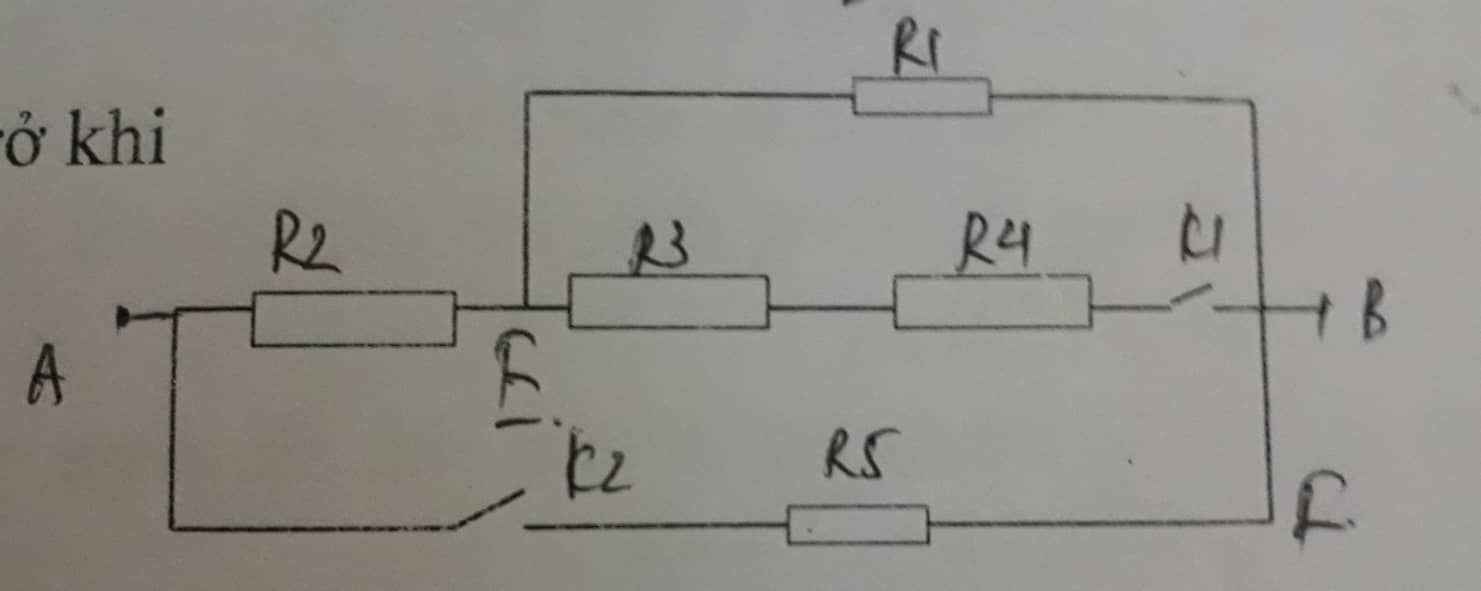
a, khi K1 đóng , K2 mở =>chỉ cần tính R2=Rtd
b,khi k1 mở,k2 đóng =>Rtd=R3
c,khi k1,k2 mở \(=>R1ntR2\)
d,k1,k2 đóng \(=>R2ntR4\)

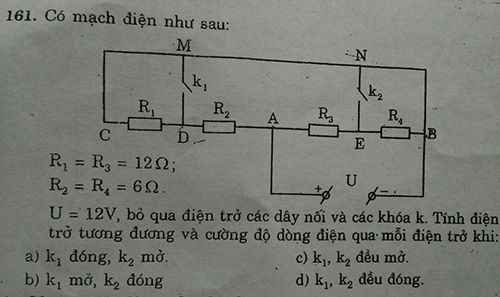
a) K1, K2 cùng mở: mạch R1 nt R2 nt R3 => Rtđ=R1+R2+R3= 90 ( ôm )
b) K1 đóng, K2 mở: (R1//R2)nt R3 => \(R_{tđ}=\dfrac{R1.R2}{R1+R2}+R3=\dfrac{9}{2}\left(\Omega\right)\)
c) K1 mở K2 đóng: (R3//R2)ntR1 => \(R_{tđ}=\dfrac{R3.R2}{R3+R2}+R1=\dfrac{9}{2}\left(\Omega\right)\)
d) K1 và K2 cùng đóng R1//R2//R3 => \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}\Rightarrow R_{tđ}=1\left(\Omega\right)\)

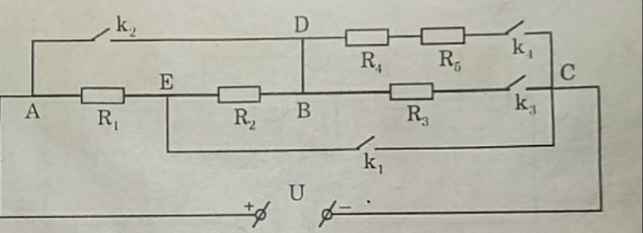
bài 1 ( nhx R nào mình ko nhắc đến thì có nghĩa nó ko có cđ dđ qua bn nhé)
a, mạch vẽ lại R2ntR1
\(R_{tđ}=2+6=8\left(\Omega\right)\)
\(I_1=I_2=\dfrac{9}{8}=1,125\left(A\right)\)
b, (R1ntR2)//R5
\(R_{tđ}=\dfrac{8.10}{18}=\dfrac{40}{9}\left(\Omega\right)\)
\(I_1=I_2=\dfrac{9}{8}=1,125\left(A\right)\)
\(I_5=\dfrac{9}{10}=0,9\left(A\right)\)
c, R2nt[(R3ntR4)//R1]
\(R_{tđ}=6+\dfrac{2.14}{16}=7,75\left(\Omega\right)\)
\(I_2=\dfrac{9}{7,75}=\dfrac{36}{31}\left(A\right)\)
\(U_{134}=9-\dfrac{36}{31}.6\approx2\left(V\right)\)
\(I_3=I_4=\dfrac{2}{14}=\dfrac{1}{7}\left(A\right)\)
\(I_1=\dfrac{2}{2}=1\left(A\right)\)
d, mạnh như hình
\(R_{AB}=7,75\left(\Omega\right)\)
\(R_{tđ}=\dfrac{10.7,75}{17,75}=\dfrac{310}{71}\)
I1 I2 I3 I4 như ý c
\(I_5=\dfrac{9}{10}=0,9\left(A\right)\)