Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
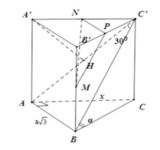
+) Ta có:
![]()
![]()
![]()
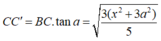
![]()
Ta có:
![]()
![]()
+) Gọi P là trung điểm của B’C’, suy ra:
(MNP)//(ABC')
![]()
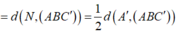
![]()
![]()
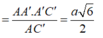
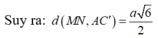

Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và \(AH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Áp dụng định lý Pitago cho tam gaics vuông AA'H:
\(A'H=\sqrt{A'A^2-AH^2}=\dfrac{3a}{2}\)
\(V=A'A.S_{ABC}=\dfrac{3a}{2}.\dfrac{a^2\sqrt{3}}{4}=\dfrac{3a^3\sqrt{3}}{8}\)

A H B C A' B' C' K I
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)

Chọn A
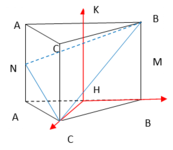
Gọi H, K lần lượt là là trung điểm cạnh A'B' và AB. Từ giả thiết ta có
![]()
![]()
Mặt khác: HC', HB' và HK đôi một vuông góc nhau.
Tọa độ hóa
![]()
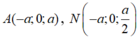
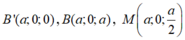
Xét mặt phẳng (BC'N) có
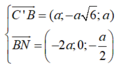
![]()
Phương trình (BC'N) là:
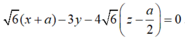
Khoảng cách từ M đến (BC'N) là:
![]()
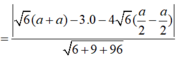

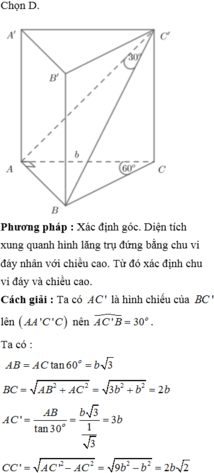
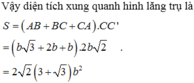

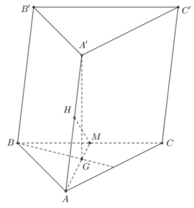

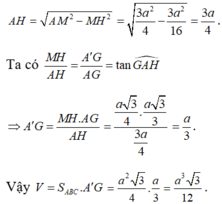
Chọn B