Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để giải bài toán này, ta sẽ sử dụng định luật Snell-Descartes về khúc xạ ánh sáng khi đi qua mặt phân cách giữa hai môi trường khác nhau. Theo đó, ánh sáng đi từ môi trường có chỉ số khúc xạ ni1, góc tới i1, đi qua mặt phân cách và khúc xạ sang môi trường có chỉ số khúc xạ ni2, góc khúc xạ r2, thì ta có công thức:
ni1sin(i1) = ni2sin(r2)
Trong đó, i1 là góc tới của ánh sáng so với pháp tuyến của mặt phân cách, r2 là góc khúc xạ của ánh sáng so với pháp tuyến của mặt phân cách.
Áp dụng định luật Snell-Descartes vào bài toán này, ta có:
Gọi n là chỉ số khúc xạ của lăng kính tam giác đều ABC. Theo đó, ánh sáng đi từ không khí (chỉ số khúc xạ ni1 = 1) vào trong lăng kính (chỉ số khúc xạ ni2 = n), góc tới của ánh sáng so với mặt phân cách AB là 60 độ (do ánh sáng chiếu qua A và hợp với mặt bên AB tạo thành góc 60 độ), ta có:1sin(60) = nsin(r2)
Gọi góc ló của ánh sáng khi ra khỏi lăng kính là α, góc lệch của ánh sáng so với phương thẳng đứng là β. Ta có:α + β = 90 độ
Ánh sáng khi ra khỏi lăng kính sẽ đi tiếp trong không khí (chỉ số khúc xạ ni1 = 1), góc tới so với pháp tuyến của mặt phân cách AB là góc lệch β, góc khúc xạ so với pháp tuyến của mặt phân cách AB là góc ló α. Ta có:n*sin(α) = sin(β)
Từ hai phương trình trên, ta suy ra:
sin(α) = (1/n)sin(60) và sin(β) = nsin(α) = sin(60)/sin(i2)
Trong đó, i2 là góc tới của ánh sáng so với pháp tuyến của mặt phân cách AB.
Để tính được góc ló và góc lệch, ta cần tìm góc i2. Ta có:
i2 = 180 - 60 - α = 120 - α
Vậy:
sin(i2) = sin(120 - α) = sin(120)*cos(α) - cos(120)*sin(α) = (sqrt(3)/2)*cos(α) - (1/2)*sin(α)

Đáp án cần chọn là: B
Theo bài ra: i 1 = 45 0 , n = 2
sin i 1 = n sin r 1 ⇒ sin 45 0 = 2 sin r 1 ⇒ r 1 = 30 0 ⇒ r 2 = A – r 1 = 30 0
n sin r 2 = sin i 2 ⇒ 2 sin 30 0 = sin i 2 ⇒ i 2 = 45 0
Góc lệch: D = ( i 1 + i 2 ) – A = 30 0

Do tính đối xứng nên: r 1 = r 2 = A 2 = 30 °
Ta có: sin i 1 = n sin r 1 . Thế số: sin i 1 = n sin r 1 = 2 sin 30 0 = 2 2 = > i 1 = 45 0 = i 2
Góc lệch: D = i 1 + i 2 - A = 45 + 45 - 60 = 30 °

Do tính đối xứng nên:
r 1 = r 2 = A 2 = 30 ° i 1 = i 2 = A + D 2 = 60 + 30 2 = 45 °
Ta có: sin i 1 = n sin r 1 ⇒ n = sin i 1 sin r 1 = sin 45 0 sin 30 0 = 2 2. 1 2 = 2

Áp dụng công thức lăng kính trong trường hợp góc chiết quang và góc tới nhỏ ta có góc lệch của tia ló và tia tới
![]()

Đáp án cần chọn là: A
Vì chiếu tia tới vuông góc với mặt nên i 1 = 0 → r 1 = 0
Ta có: A = r 1 + r 2 → A = r 2
Mà: D = i 1 + i 2 − A ↔ 15 = 0 + i 2 − A → i 2 = 15 + A
Lại có:
sin i 2 = n sinr 2 ↔ sin i 2 = n sin A ↔ sin ( 15 + A ) = 1,5 sin A
↔ sin 15 c osA + sinAcos 15 = 1,5 sin A
↔ sin 15 c osA = ( 1,5 − cos 15 ) sinA
→ tan A = sin 15 1,5 − c os 15 = 0,485 → A = 25,87

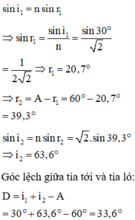
Sử dụng công thức chiết suất của chất trong môi trường khác nhau:
n1 * sin(i) = n2 * sin®
Trong đó:
n1 là chỉ số khúc xạ của chất ở môi trường ban đầu (ở đây là không khí, n1 = 1)i là góc giữa tia sáng và pháp tuyến của mặt phân cách giữa hai môi trường (ở đây là góc chiếu qua A)n2 là chỉ số khúc xạ của chất ở môi trường mới (ở đây là lăng kính tam giác đều ABC, n2 = căn 2)r là góc giữa tia sáng và pháp tuyến của mặt phân cách giữa hai môi trường (ở đây là góc ló)Ta có: i = 90 - 30 = 60 độ (do góc chiếu qua A hợp với mặt bên AB một góc 30 độ)
n1 = 1
n2 = căn 2
Vậy ta có: sin(60) = căn 3/2
n1 * sin(i) = n2 * sin®
1 * căn 3/2 = căn 2 * sin®
sin® = căn 3/4
Do đó, góc ló là: r = arcsin(căn 3/4) = 48,6 độ (là góc giữa tia sáng và pháp tuyến của mặt bên AB)
Để tính góc lệch, ta sử dụng công thức:
góc lệch = góc ló - góc chiếu qua A = 48,6 - 60 = -11,4 độ
Vậy góc ló là 48,6 độ và góc lệch là -11,4 độ.