Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có thể tích của khối lăng trụ: V= h.Sđáy= 6.10 = 60 cm3→ Đáp án C


a) Gọi \(I\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều \( \Rightarrow AI \bot BC\)
Tam giác \(A'BC\) cân tại \(A' \Rightarrow A'I \bot BC\)
\( \Rightarrow \left( {\left( {A'BC} \right),\left( {ABC} \right)} \right) = \left( {A'I,AI} \right) = \widehat {AI{\rm{A}}'} = {60^ \circ }\)
Tam giác \(ABC\) đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\( \Rightarrow AA' = AI.\tan \widehat {AI{\rm{A}}'} = \frac{{3a}}{2}\)
b) \({S_{\Delta ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{{a^2}\sqrt 3 }}{4}\)
\({V_{ABC.A'B'C'}} = {S_{\Delta ABC}}.AA' = \frac{{3{a^3}\sqrt 3 }}{8}\)

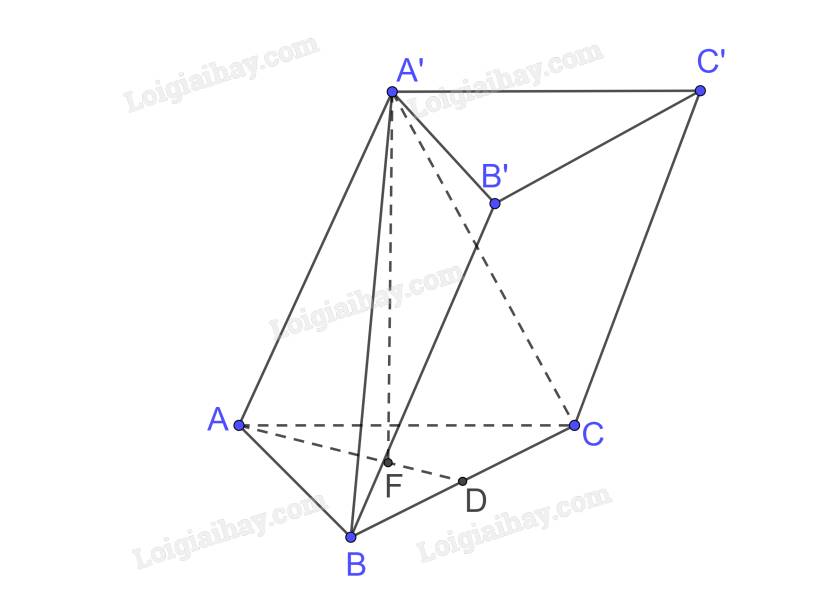
Vì hình chóp A’.ABC có A'A = A'B = A'C và đáy ABC là tam giác đều nên hình chóp A’.ABC đều.
Gọi F là hình chiếu của A’ trên (ABC) nên F là tâm của đáy ABC là tam giác đều do đó F cũng là trọng tâm của tam giác ABC.
Gọi AF cắt BC tại D
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà F là trọng tâm nên \(AF = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác A’AF vuông tại F có
\(A'F = \sqrt {A'{A^2} - A{F^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Diện tích tam giác đều ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối lăng trụ là \(V = A'F.S = \sqrt {{b^2} - \frac{{{a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}\)
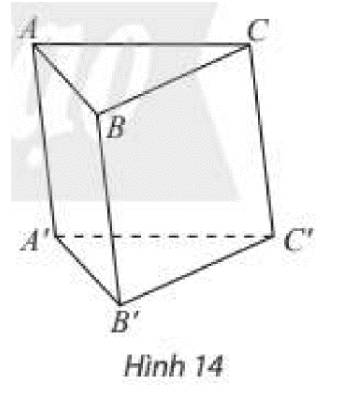
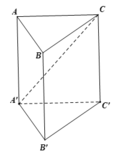
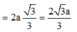
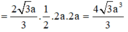

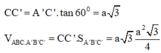
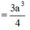
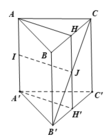
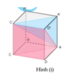
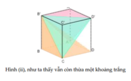
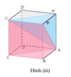
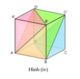

Chúng ta sẽ chia thành 3 khối như sau:
A.A'B'C', B'.ABC và C.A'B'C'
tham khảo:
Ba tứ diện A'.ABC, C.A'B'B, C.A'B'C' có cùng chiều cao và diện tích đáy.