Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A.
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A ' B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' Q B ' B + D N D ' D = 7 2
Do đó thể tích khối đa diện nhỏ hơn là 15 2 V = 5 2 .2018 = 5045 6 .
Đáp án A
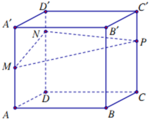
Cho lăng trụ A B C D . A ' B ' C ' D ' có A M = a , B N = b , C P = c , S = S A B C .
Khi đó V M N P . A B C = a + b + c 3 . S
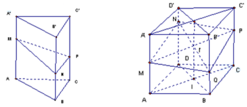
Đặt A A ' = a ⇒ A M = a 2 , P C = 2 a 3 ;
Ta có D N + B Q = 2 I I ' = M A + P C = 7 a 6 ; S A B D = S C B D = S
Áp dụng tính chất có
V M N P Q . A B C D = V M N P . A D B + V N Q P . C B C = 1 3 A M + B Q + D N . S + 1 3 D N + B Q + C P . S = 1 3 3 A M + 3 P C . S = 7 6 a . S = 7 12 V A B C D . A ' B ' C ' D ' ⇒ V A ' B ' C ' D ' . M N P Q = 5 12 V A B C D . A ' B ' C ' D ' = 5 12 .2018 = 5045 6
Phương pháp:
- Dựng mặt phẳng chứa B'G và song song với C'D.
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Cách giải:
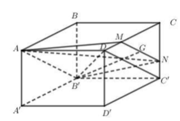
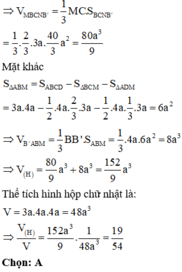
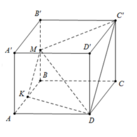
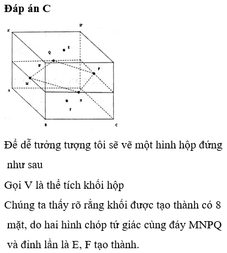
Chuẩn hóa hình hộp đã cho là hình lập phương cạnh a.
Dựng M K / / A B ' / / C ' D
Khi đó thiết diện là tứ giác
Ta có: V 1 = 1 3 h S 1 + S 1 S 2 + S 2
Trong đó h = H B = a ' S 1 = S B M K = a 2 8 ; S 2 = S C ' D C = a 2 2
Do đó V 1 = 7 24 a 3 ⇒ V 2 = a 3 − V 1 = 17 24 a 3
Vậy V 1 V 2 = 7 17
Đáp án B
Đáp án A
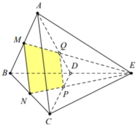
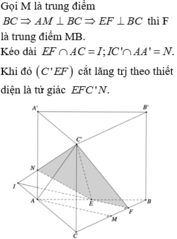
Nối 
chia khối tứ diện ABCD thành hai khối đa diện gồm PQD.NMB và khối đa diện chứa đỉnh A có thể tích A.
Dễ thấy P,Q lần lượt là trọng tâm của ∆BCE, ∆ABE
Gọi S là diện tích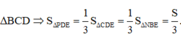 
Họi h là chiều cao của tứ diện ABCD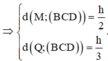 
Khi đó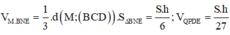 
Suy ra
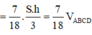
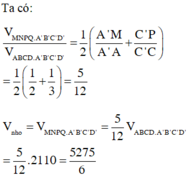
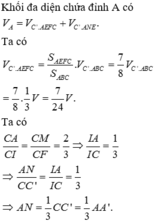
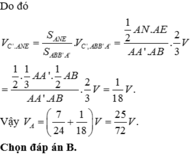
Chọn A