
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




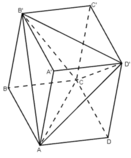
Gọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện ACB’D’ và bốn khối chóp A.A’B’D’, C.C’B’D’, B’.BAC và D’. DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng và chiều cao bằng h, nên tổng các thể tích của chúng bằng
.
Từ đó suy ra thể tích của khối tứ diện
ACB’D’=. Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện ACB’D’ bằng 3.
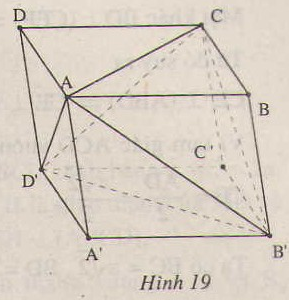

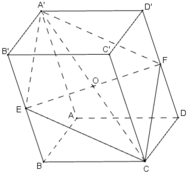
Gọi O là tâm hình hộp và tâm của hình bình hành BB’D’D. Khi đó O là trung điểm của EF.
Ta có: A’ ∈ CO (1)
CO ⊂ mp(CEF)(2)
Mặt khác A’E // CF, A’F // CE
Nên mp(CEF) cắt hình hộp theo thiết diện là hình bình hành A’ECF.
mp(CEF) chia hình hộp ABCD.A’B’C’D’ thành hai khối đa diện (Đ) và (Đ’).
Gọi (Đ) là khối đa diện có các đỉnh là A, B, C, D, A’, E, F và (Đ’) là khối đa diện còn lại.
Phép đối xứng qua tâm O biến các đỉnh A, B, C, D, A’, E, F của đa diện (Đ) lần lượt thành các đỉnh C’, D’, A’, B’, C, F, E của khối da diện (Đ’)
Suy ra phép đối xứng qua tâm O biến (Đ) thành (Đ’), nghĩa là hai hình đa diện (Đ) và (Đ’) bằng nhau.
Vậy tỉ số thể tích của (Đ) và (Đ’) bằng 1.

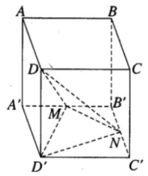
Thể tích khối chóp D’.DMN bằng thể tích khối chóp D.D’MN
Ta có: S D ' MN = S A ' B ' C ' D ' - S D ' A ' M + S D ' C ' N + S B ' MN
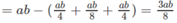
Thể tích khối chóp
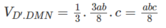
Từ đó suy ra tỷ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng 1/8

Phương pháp:
Phân chia khối hộp ra các phần, lập tỉ số thể tích.
Cách giải:

Gọi V là thể tích khối hộp ABCD.A'B'C'D'
Ta có: ![]()
= 1 6 V
Mà ![]()
![]()
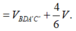
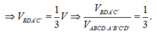
Chọn: C

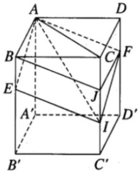
Giả sử (AEF) cắt CC’ tại I. Khi đó ta có AE// FI, AF // EI nên tứ giác AEIF là hình bình hành. Trên cạnh CC’ lấy điểm J sao cho CJ = DF. Vì CJ song song và bằng DF nên JF song song và bằng CD. Do đó tứ giác CDFJ là hình chữ nhật. Từ đó suy ra FJ song song và bằng AB. Do đó AF song song và bằng BJ. Vì AF cũng song song và bằng EI nên BJ song song và bằng EI.
Từ đó suy ra IJ = EB = DF = JC = c/3
Ta có
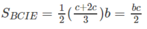
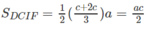
Nên V H = V A . BCIE + V A . DCIF
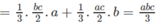
Vì thể tích khối hộp chữ nhật ABCD.A’B’C’D’ bằng abc nên
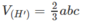
Từ đó suy ra