Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S B M H A E N C D
Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??

Gọi O là tâm đáy \(\Rightarrow SO=\sqrt{SA^2-OC^2}=\sqrt{SA^2-\left(\frac{AC}{2}\right)^2}=\frac{a\sqrt{6}}{2}\)
Gọi I là điểm sao cho \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}+\overrightarrow{IS}=0\)
\(\Leftrightarrow4.\overrightarrow{IO}+\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{IS}=0\)
\(\Leftrightarrow4\overrightarrow{IO}+\overrightarrow{IS}=0\Rightarrow\overrightarrow{IO}=-\frac{1}{4}\overrightarrow{IS}\)
\(\Rightarrow I\) nằm trên đoạn thẳng SO và chia SO theo tỉ lệ \(IO=\frac{1}{4}IS\Rightarrow IS=\frac{4}{5}SO=\frac{2a\sqrt{6}}{5}\)
Ta có:
\(Q=MA^2+MB^2+MC^2+MD^2+MS^2\)
\(=\left(\overrightarrow{MI}+\overrightarrow{IA}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IB}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IC}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{ID}\right)^2+\left(\overrightarrow{MI}+\overrightarrow{IS}\right)^2\)
\(=5MI^2+IA^2+IB^2+IC^2+ID^2+IS^2\)
Mà I cố định \(\Rightarrow Q_{min}\) khi và chỉ khi \(MI_{min}\)
\(\Rightarrow\) M là hình chiếu vuông góc của I lên (SCD)
A B C D S O I M N
Gọi N là trung điểm CD, kẻ \(IM\perp SN\Rightarrow IM\perp\left(SCD\right)\)
\(SN=\sqrt{SO^2+ON^2}=\frac{a\sqrt{7}}{2}\Rightarrow SM=SI.cos\widehat{NSI}=\frac{SI.SO}{SN}=\frac{12a\sqrt{7}}{35}\)
\(\Rightarrow\frac{d\left(M;\left(ACD\right)\right)}{SO}=1-\frac{SM}{SN}=1-\frac{24}{35}=\frac{11}{35}\)
\(\frac{S_{ACD}}{S_{ABCD}}=\frac{1}{2}\)
\(\Rightarrow\frac{V_2}{V_1}=\frac{d\left(M;\left(ACD\right)\right).S_{ACD}}{SO.S_{ABCD}}=\frac{11}{35}.\frac{1}{2}=\frac{11}{70}\)

S B C D A M N
Ta có : MN là đường trung bình của tam giác SAD
Suy ra MN song song với AD và \(MN=\frac{1}{2}AD\Rightarrow\begin{cases}MN||BC\\MN=BC\end{cases}\)\(\Rightarrow\) BCNM là hình bình hành (1)
Mặt khác
\(\begin{cases}BC\perp AB\\BC\perp SA\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp BM\left(2\right)\)
Từ (1) và (2) ra suy ra BCNM là hình chữ nhật
Ta có :
\(S_{BCNM}=2S_{\Delta BCM}\Rightarrow V_{S.BCNM}=2V_{S.BCM}\)
\(V_{S.BCM}=V_{C.SBM}=\frac{1}{3}CB.S_{\Delta SBM}=\frac{1}{6}CB.S_{\Delta SAB}=\frac{1}{6}CB.\frac{1}{2}SA.AB=\frac{a^3}{6}\)
Vậy \(V_{S.BCNM}=\frac{a^3}{3}\)

S A B C D M N H K
Thế tích của khối chóp S.CDNM :
\(S_{CDNM}=S_{ABCD}-S_{AMN}-SBC\)
\(=AB^2-\frac{1}{2}AM.AN-\frac{1}{2}BC.BM\)
\(=a^2-\frac{a^2}{8}-\frac{a^2}{4}=\frac{5a^2}{8}\)
Vậy \(V_{SCDNM}=\frac{1}{3}S_{CDNM.SH}=\frac{5\sqrt{3}a^2}{24}\)
Khoảng cách giữa 2 đường thẳng DM và SC
\(\Delta ADM=\Delta DCN\Rightarrow\widehat{ADM}=\widehat{DCN}\Rightarrow DM\perp CN\)
Kết hợp với điều kiện :
\(DM\perp SH\Rightarrow DM\perp\left(SHC\right)\)
Hạ \(HK\perp SC\left(K\in SC\right)\Rightarrow HK\)là đoạn vuông góc chung của DM và SC
Do đó :
\(d\left(DM,SC\right)=HK\)
Ta có :
\(\begin{cases}HC=\frac{CD^2}{CN}=\frac{2a}{\sqrt{5}}\\HK=\frac{SH.HC}{\sqrt{SH^2+HC^2}}=\frac{2\sqrt{3}a}{\sqrt{19}}\end{cases}\)
\(\Rightarrow d\left(DM,SC\right)=\frac{2\sqrt{3}a}{\sqrt{19}}\)
cậu ơi, hướng dẫn giúp tớ bài tương tự này với: cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, góc giữa SD và mặt phẳng ABCD là 45 độ, SA vuông góc (ABCD). M là trung điểm BC. Tính khoảng cách DM và SC
cảm ơn c nhiều nhiều.

A B C D S M H
\(\widehat{BAD}=120^0\Rightarrow\widehat{ABC}\Rightarrow\Delta ABC\) đều
\(\Rightarrow AM=\frac{a\sqrt{3}}{2}\Rightarrow S_{ABCD}=\frac{a^3\sqrt{3}}{2}\)
Tam giác SAM vuông tại A có \(\widehat{SMA}=45^0\Rightarrow\) Tam giác SAM vuông tại A : SA = AM = \(\frac{a\sqrt{3}}{2}\)
Do đó \(V_{S.ABCD}=\frac{1}{3}SA.S_{ABCD}=\frac{a^3}{4}\)
Do AD song song với BC nên d(D;(SBC))=d(A,(SBC))
Gọi H là hình chiếu vuông góc của A trên SM
Ta có : \(\begin{cases}AM\perp BC\\SA\perp BC\end{cases}\)\(\Rightarrow BC\perp\cdot\left(SAM\right)\)
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow d\left(A,\left(SBC\right)\right)=AH\)
Ta có :
\(AH=\frac{AM\sqrt{2}}{2}=\frac{a\sqrt{6}}{4}\Rightarrow d\left(D,\left(SBC\right)\right)=\frac{a\sqrt{6}}{4}\)


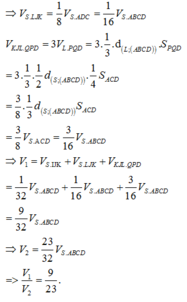
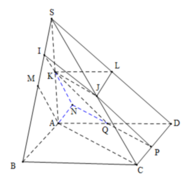
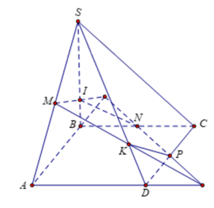
Kéo dài MN cắt AD và AB lần lượt tại E và F, nối PE cắt SD tại K và PF cắt SB tại Q \(\Rightarrow PQMNK\) là tiết diện của (MNP) và chóp.
Gọi thể tích chóp là \(V\) , khoảng cách từ S xuống đáy là \(h\) và giả định phần dưới là \(V_1\) cho dễ gọi tên
\(V_1=V_{PAEF}-V_{KDEN}-V_{QBME}\)
\(S_{DEN}=S_{BMF}=S_{MNC}=\frac{1}{8}S_{ABCD}\Rightarrow S_{AEF}=\frac{9}{8}S_{ABCD}\)
\(\Rightarrow V_{PAEF}=\frac{1}{3}.\frac{h}{2}.S_{AEF}=\frac{9}{16}\frac{1}{3}hS_{ABCD}=\frac{9}{16}V\)
Áp dụng định lý Menelaus: \(\frac{PS}{PA}.\frac{EA}{ED}.\frac{KD}{KS}=1\Rightarrow1.\frac{3}{1}.\frac{KD}{KS}=1\)
\(\Rightarrow KS=3KD\Rightarrow KD=\frac{1}{4}SD\Rightarrow d\left(K;\left(ABCD\right)\right)=\frac{1}{4}d\left(S;\left(SBCD\right)\right)=\frac{h}{4}\)
\(\Rightarrow V_{KDEN}=V_{QBME}=\frac{1}{3}.\frac{h}{4}.\frac{1}{8}S_{ABCD}=\frac{1}{32}.\left(\frac{1}{3}hS_{ABCD}\right)=\frac{V}{32}\)
\(\Rightarrow V_1=\frac{9}{16}V-2.\frac{V}{32}=\frac{V}{2}\)
\(\Rightarrow V_1=V_2=\frac{V}{2}\)