Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) BC vuông góc với AO là theo tính chất hai tiếp tuyến đi qua 1 điểm A
b) Xét hai tam giác DCO và DBA có góc D chung và góc C = góc B = 90 độ (tính chất tiếp tuyến)
=> tam giác DCO đồng dạng với tam giác DBA
=> DC/DB = DO/DA
=> DC.DA = DO.DB (đpcm)
c) Vì OM vuông góc với DB => OM // BA (cùng vuông góc với DB)
Ta có AM/DM + 1 = (AM + DM)/DM = DA/DM
Theo Viet ta có: DA/DM = AB/MO
=> AM/DM + 1 = AB/OM
=> AB/OM - AM/DM = 1 (*)
Ta lại có tam giác MOA cân (vì góc MOA = góc BAO do so le trong, góc MAO = góc BAO do tính chất hai tiếp tuyến cùng 1 điểm)
=> OM = AM
(*) trở thành: AB/AM - AM/DM = 1 (đpcm)
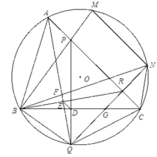
2). Gọi PQ giao BC tại D, AQ giao BR tại E ta có các biến đổi góc sau
E Q D ^ = D Q B ^ − A Q B ^ = P R B ^ − A C B ^ = R B C ^ = E B D ^ .
Vậy tứ giác BEDQ nội tiếp, suy ra B E Q ^ = B D Q ^ = 90 0 ⇒ B R ⊥ A Q
Có 2 tam giác vuông \(\Delta ABE=\Delta ADF\) vì \(AB=AD\) và \(\widehat{BAE}=\widehat{DAF}\) cùng phụ với \(\widehat{DAE}\)
Suy ra tam giác AEF vuông cân và \(ME=MA=MF\Rightarrow AM\perp EF\)
Ta có \(\overrightarrow{MA}=\left(2;-4\right)\), đường thẳng EF đi qua M có phương trình :
\(2\left(x+4\right)-4\left(y-2\right)=0\Leftrightarrow x-2y+8=0\)
Bây giờ tìm tọa độ các điểm E, F thỏa mãn ME=MA=MF. Gọi T(x;y) thuộc đường thẳng EF, thì x=2t-8; y=t, \(t\in R\)
Khi đó \(MT=MA\Leftrightarrow\left(2t-8+4\right)^2+\left(1-2\right)^2=2^2+\left(-4\right)^2=20\)
\(\Leftrightarrow5\left(t-2\right)^2=20\Leftrightarrow t\left(t-4\right)=0\Leftrightarrow\)\(\begin{cases}t=0\\t=4\end{cases}\)
Như vậy có 2 điểm \(t_1\left(-8;0\right);t_2\left(0;4\right)\) ( Chính là 2 điểm E và F) thuộc đường thẳng EF mà \(MT_1=MA\)
- Trường hợp \(E\left(-8;0\right);F\left(0;4\right)\). Do F thuộc đường thẳng CD nên đường thẳng CD nhận \(\overrightarrow{KF}=\left(3;4\right)\) làm vec tơ chỉ phương.
Phương trình đường thẳng CD là \(\begin{cases}x=3t\\y=4+4t\end{cases}\) (\(t\in R\)).
Khi đó \(D\left(3t;4+4t\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{KF}.\overrightarrow{AD}=0\Rightarrow3\left(3t+6\right)+4\left(-2+4t\right)=0\Leftrightarrow t=-\frac{2}{5}\Rightarrow D\left(-\frac{6}{5};\frac{12}{5}\right)\)
- Trường hợp \(F\left(-8;0\right);E\left(0;4\right)\), đường thẳng CD nhận \(\overrightarrow{FK}=\left(5;0\right)\) làm vec tơ chỉ phương
Phương trình CD : \(\begin{cases}x=-8+5t\\y=0\end{cases}\) \(\left(t\in R\right)\)
Khi đó \(D\left(-8+5t;0\right)\)
Ta có \(AD\perp KF\Leftrightarrow\overrightarrow{FK}.\overrightarrow{AD}=0\Leftrightarrow5\left(-2+5t\right)=0\Leftrightarrow t=\frac{2}{5}\Rightarrow D\left(-6;0\right)\)
.
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác .