Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: ΔAEF vuông cân tại A
Xét ΔADF vuông tại D và ΔABE vuông tại B có
AD=AB
DF=BE
Do đó: ΔADF=ΔABE
=>AF=AE và \(\widehat{DAF}=\widehat{BAE}\)
mà \(\widehat{BAE}+\widehat{DAE}=90^0\)
nên \(\widehat{DAF}+\widehat{DAE}=90^0\)
=>\(\widehat{FAE}=90^0\)
Xét ΔAEF có \(\widehat{FAE}=90^0\) và AE=AF
nên ΔAEF vuông cân tại A
b: Gọi giao điểm của AH với EF là M
H đối xứng A qua EF
=>EF là đường trung trực của HA
=>EH=EA và FH=FA
mà AH=AE
nên EH=EA=FH=FA
Xét tứ giác AEHF có
AE=HE=HF=FA
nên AEHF là hình thoi
Hình thoi AEHF có \(\widehat{FAE}=90^0\)
nên AEHF là hình vuông

Bài 1
A A A B B B C C C H H H M M M D D D I I I a/Xét tứ giác BHCD có M đồng thời là trung điểm của cả HD và BC
Do đó BHCD là hình bình hành \(\Rightarrow BH//CD,CH//BD\)
Mặt khác vì ta có H là trực tâm của tam giác ABC nên \(BH\perp AC,CH\perp AB\)
Suy ra \(BD\perp AB,CD\perp AC\Rightarrow\Delta ABD,\Delta ACD\)là tam giác vuông
b/Xét \(\Delta ABD,\Delta ACD:\widehat{ABD}=\widehat{ACD}=90^0\);I là trung điểm của cạnh huyền chung AD
Suy ra \(IA=IB=IC=ID\)
Bài 2 α = 60° α = 60° α = 60° A A A B B B C C C D D D E E E a/Vì AD=CD(gt) nên D nằm trên trung trực của đoạn AC suy ra \(\widehat{DAC}=\widehat{ECA}=90^0-60^0=30^0\)
Suy ra \(\widehat{BAD}=90^0+\widehat{DAC}=120^0\)
b/Trước hết ta thấy ABCD đã là hình thang,nên ta đi chứng minh \(\widehat{BCD}=\widehat{ABC}=60^0\)
Ta có \(\widehat{BCD}=\widehat{DCA}+\widehat{ACB}=\widehat{DAC}+30^0=30^0+30^0=60^0\)
Vậy ABCD là hình thang cân
c/Ta có \(\Delta BCE:AE=BE,\widehat{ABE}=60^0\Rightarrow AE=BE=AB\)
\(\widehat{ADE}=\frac{1}{2}.\widehat{ADC}=60^0;\widehat{BAD}=120^0=\widehat{BED}\)
Suy ra ABED là hình bình hành
Mà ta còn có AB=EB
Vậy ABED là hình thoi

a) DDAE = DBAF (c.g.c)
⇒ D A E ^ = B A F ^ và AE = AF
Mà E A D ^ + E A B ^ = 90 0 = > E A B ^ + B A F ^ = 90 0
Þ DAEF vuông cân tại A.
b) DEAF vuông cân nên IA = IE = FI (1); DCFE vuông có IC là đường trung tuyến Þ IE = IC = IF (2);
Từ (1) và (2) suy ra Þ IA = IC nên I thuộc trung trực của AC hay I thuộc BD.
c) Do K đối xứng với A qua I nên I là trung điểm của AK.
Mà I là trung điểm của EF(gt) nên AFKE là hình bình hành, DAEF vuông cân tại A nên AI ^ EF.
Vậy AFKE là hình vuông.
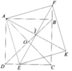

a, Xét 2 tam giác vuông ΔADE và ΔABF có:
AD = AB (ABCD là hình vuông); DE = BF (gt)
⇒ ΔADE = ΔABF (2 cạnh góc vuông)
⇒ AE = AF (1) và ˆDAEDAE^ = ˆBAFBAF^
mà ˆDAEDAE^ + ˆBAEBAE^ = 90o90o
⇒ ˆBAFBAF^ + ˆBAEBAE^ = 90o90o
⇒ ˆEAFEAF^ = 90o90o (2)
Từ (1) và (2) suy ra ΔEAF vuông cân (đpcm)
b, ABCD là hình vuông ⇒ BA = BC và DA = DC
⇒ BD là đường trung trực của AC (3)
ΔEAF vuông cân tại A có AI là trung tuyến ứng với cạnh huyền
⇒ AI = 1212EF
ΔCEF vuông tại C có CI là trung tuyến ứng với cạnh huyền
⇒ CI = 1212EF
⇒ CI = AI ⇒ I thuộc đường trung trực của AC (4)
Từ (3) và (4) suy ra: I thuộc BD (đpcm)
d, Tứ giác AEKF có 2 đường chéo AK, EF cắt nhau tại I là trung điểm mỗi đường
⇒ AEKF là hình bình hành
mà AE = AF và ˆEAFEAF^ = 90o90o
⇒ AEKF là hình vuông (đpcm)