K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

11 tháng 4 2023
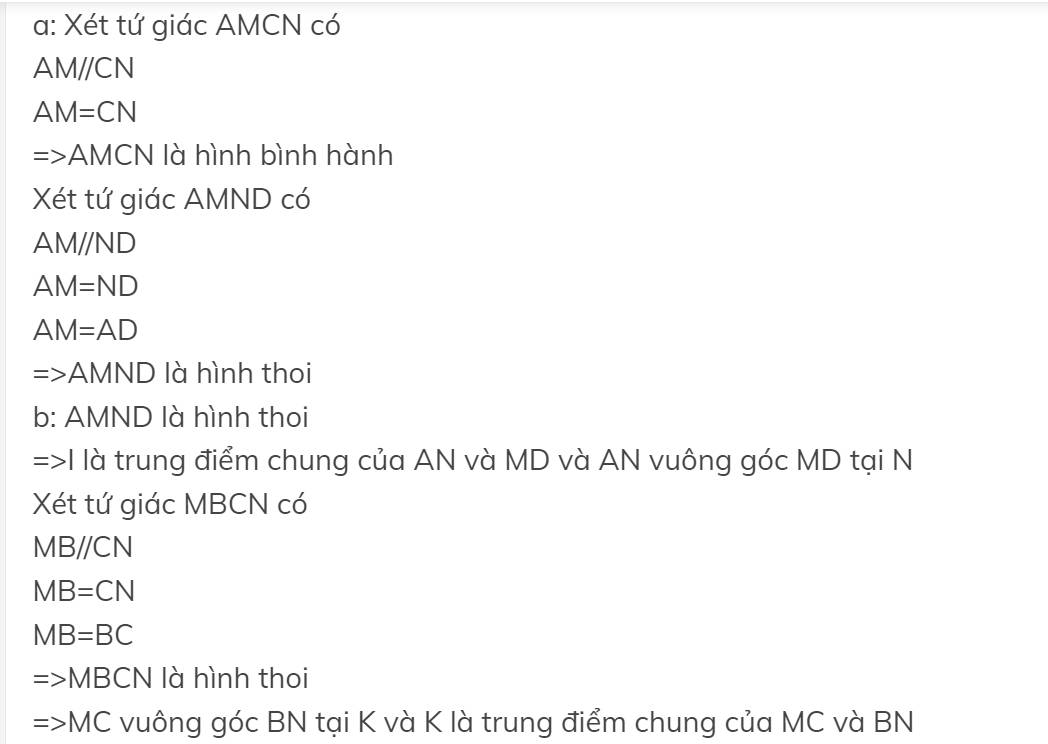
a: Xét tứ giác BMDP có
BM//DP
BM=DP
=>BMDP là hình bình hành
b: Xet ΔADH có P là trung điểm của AD và PQ//DH
=>Q là trung điểm của AH
ΔABP=ΔDAN
=>góc ABP=góc DAN
=>góc ABP+góc BAQ=90 độ
=>ΔABQ vuông tại Q
=>BQ vuông góc AH
=>ΔBAH cân tại B
=>BA=BH

16 tháng 11 2021
a: Xét tứ giác AICK có
AI//CK
AI=CK
Do đó: AICK là hình bình hành

28 tháng 3 2020
bạn ơi đầu bài có nhầm lẫn j ko làm sao bình phương của OD có thể bằng tích của DI với DM được


a)
Xét ΔvDMC và ΔvAND, ta có:
DC = AD
MC = ND ( MC = \(\dfrac{BC}{2}\) = \(\dfrac{CD}{2}\) = ND )
⇒ ΔDMC = ΔAND ( cgv-cgv )
⇒ ∠MDC = ∠NAD ( cgtứ )
Ta có: ∠CMD = ∠MDA ( slt, AB//AD )
Mà: ∠MDC + ∠CMD = 90°
⇒ ∠NAD + ∠MDA = 90°
⇒ ∠AID = 90°
Hay: AN ⊥ DM (đpcm)
b)
Gọi K là trung điểm của AD, H là giao điểm của BK và AN
Ta có: BM = KD ( BM = \(\dfrac{BC}{2}\) = \(\dfrac{AD}{2}\) = KD ); BM // KD ( BC//AD )
⇒ Tứ giác BMDK là hình bình hành
⇒ BK // MD
⇒ ∠AID = ∠BHI = 90° ( slt )
⇒ BH là đường cao của ΔBAI (1)
ΔAID có: KA = KD ( dựng hình ); HK // ID (BK//MD)
⇒ HA = HI
⇒ BH là đường trung tuyến của ΔBAI (2)
Từ (1), (2) ⇒ ΔBAI cân tại B ⇒ BA = BI (đpcm)