Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

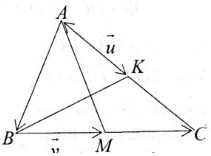
Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)

a/ \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{EF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\)
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\overrightarrow{AC}=\overrightarrow{AK}+\overrightarrow{KC}=\overrightarrow{AK}+\frac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\overrightarrow{AK}+2\overrightarrow{BM}-\frac{1}{2}\overrightarrow{BC}\Rightarrow\overrightarrow{BC}=\frac{2}{3}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}=\overrightarrow{AK}+\frac{1}{2}\left(\frac{3}{2}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\right)=...\)
\(\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BC}=...\)

A B C D O M N
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).

A B C E D G
\(\text{a) Ta có : }2\overrightarrow{CD}=3\overrightarrow{DB}\\ \Rightarrow\overrightarrow{DC}=-\frac{3}{2}\overrightarrow{DB}\\ \Rightarrow D;B;C\text{ thẳng hàng },D\text{ nằm giữa }B;C\left(\frac{3}{2}< 0\right)\\ \Rightarrow\overrightarrow{BC}=\overrightarrow{BD}+\overrightarrow{DC}=\overrightarrow{BD}+\frac{3}{2}\overrightarrow{BD}=\frac{5}{2}\overrightarrow{BD}\\ 5\overrightarrow{EB}=2\overrightarrow{EC}\\ \Rightarrow\overrightarrow{EB}=\frac{2}{5}\overrightarrow{EC}\\ \Rightarrow E;B;C\text{ thẳng hàng },B\text{ nằm giữa }E;C\left(\frac{2}{5}>0;EB< EC\right)\\ \Rightarrow\overrightarrow{BC}=\overrightarrow{EC}-\overrightarrow{EB}=\overrightarrow{EC}-\frac{2}{5}\overrightarrow{EC}=\frac{3}{5}\overrightarrow{EC}\)
\(\Rightarrow\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}\\ =\overrightarrow{AB}+\frac{2}{5}\overrightarrow{BC}=\overrightarrow{AB}+\frac{2}{5}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\\ =\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}-\frac{2}{5}\overrightarrow{AB}=\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\)
\(\overrightarrow{AE}=\overrightarrow{EC}+\overrightarrow{CA}\\ =\frac{5}{3}\overrightarrow{BC}-\overrightarrow{AC} =\frac{5}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)-\overrightarrow{AC}\\ =\frac{5}{3}\overrightarrow{AC}-\frac{5}{3}\overrightarrow{AB}-\overrightarrow{AC}=\frac{2}{3}\overrightarrow{AC}-\frac{5}{3}\overrightarrow{AB}\)
\(b\text{) Theo tính chất trọng tâm }\Delta:3\overrightarrow{AG}=\overrightarrow{AA}+\overrightarrow{AB}+\overrightarrow{AC}\\ =\overrightarrow{0}+\overrightarrow{AB}+\overrightarrow{AC}\\ =\left(\frac{9}{4}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AC}\right)-\left(\frac{1}{2}\overrightarrow{AC}+\frac{5}{4}\overrightarrow{AC}\right)\\ =\frac{15}{4}\left(\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}\right)-\frac{3}{4}\left(\frac{2}{3}\overrightarrow{AC}+\frac{5}{3}\overrightarrow{AC}\right)\\ =\frac{15}{4}\overrightarrow{AD}-\frac{3}{4}\overrightarrow{AE}\)
\(\Rightarrow\overrightarrow{AG}=\frac{5}{4}\overrightarrow{AD}-\frac{1}{4}\overrightarrow{AE}\)
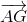 =
= 
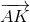 =>
=> 
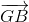 = -
= -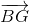 = -
= -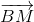 = -
= -
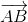 =
= 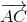 = 2
= 2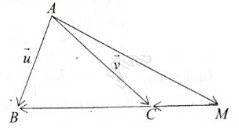
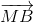 = 3
= 3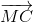 =>
=> 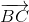 )
)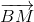 =
= 
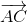 -
- 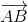 nên
nên 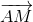 =
= 
A B C D E
Theo tính chất trung điểm
\(\overrightarrow{AE}=\dfrac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{AC}\right)=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\)\(=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)\)\(=\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}=\overrightarrow{u}+\dfrac{1}{2}\overrightarrow{v}\).