Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có S(OMC) = 1/8 S(ABCD) = 1/8 ; S(OBC) = 1/4 S(ABCD) = 1/4
=> S(OMC)/S(OBC) = 1/8 : 1/4 = 1/2
Mà hai tam giác có chung cạnh OC => Đường cao hạ từ M xuống OC bằng 1/2 đường cao hạ từ B xuống MC
=> S(MQC) = 1/2 S(QMC) (*)
Ta có S(MCB) = 1/4 S(ABCD) = 1/4
=> S(MQC) + S(QMC) = S(MCB) = 1/4 (**)
Từ (*) và (**) suy ra S(MQC) = 1/4 : 3 = 1/12
Do tính chất đối xứng, S(MPD) = 1/12
=> S(MPOQ) = S(ODC) - S(MQC) - S(MPD) = 1/4 - 1/12 - 1/12 = 1/12
Đáp số: 1/12

Đáp án D.
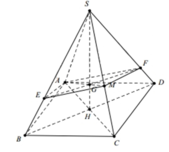
Gọi H là tâm của hình vuông A B C D ; S B H ^ = 60 0 ; H B = a 2 2
Khi đó là trọng tâm tam giác SAC.
Qua G dựng đường thẳng song song với BD cắt SB;SD lần lượt là E và F.
Do tính chất đối xứng ta có:
V S . A E M F V S . A B C D = V S . A E M V S . A B C = S E S B . S M S C = 2 3 . 1 2 = 1 3 .
Mặt khác V A . A B C D = 1 3 S H . S A B C D = 1 3 H B tan 60 0 . a 2 = a 3 6 6 .
Do đó V S . A E M F = 1 3 . a 3 6 6 = a 3 6 18 .

Chọn B.
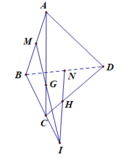
M G ⊂ A B C N H ⊂ B C D A B C ∩ B C D = B C N H ∩ M G = I ⇒ I ∈ B C
vậy B, I, C thẳng hàng

Đáp án D
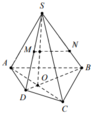
Dựa vào hình vẽ, ta thấy 2 đường thẳng MN và SO cắt nhau. Các cặp đường thẳng (SO;AD),(MN;SC),(SA;BC) chéo nhau


Bài toán 93 trên OLM đây mà!
Không có hình thì giải bài kiểu gì?