Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d\left(A\left(P\right)\right)=\frac{\left|2\left(-2\right)-2.1+1.5-1\right|}{\sqrt{2^2+\left(-2\right)^2+1^2}}=\frac{2}{3}\)
(P) có vectơ pháp tuyến là \(\overrightarrow{n_p}=\left(2;-2;1\right);\)
d có vectơ pháp tuyến là \(\overrightarrow{u_d}=\left(2;3;1\right);\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(-5;0;10\right)\)
Theo giả thiết suy ra (Q) nhận \(\overrightarrow{n}=-\frac{1}{5}\left[\overrightarrow{n_p},\overrightarrow{u_d}\right]=\left(1;0;-2\right)\) làm vectơ pháp tuyến
Suy ra \(\left(Q\right):x-2z+12=0\)

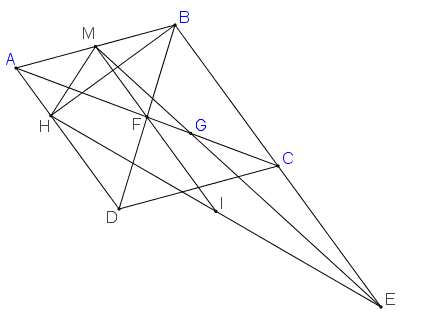
a) Ta có góc BEC = góc BDC = 90o (góc nội tiếp chắn giữa đường tròn)
Suy ra BD \(\perp\) AC và CE \(\perp\) AB. Mà BD cắt CE tại H là trực tâm \(\Delta\) ABC.
Suy ra AH \(\perp\) BC
Vì AH \(\perp\) BC, BD \(\perp\) AC nên góc HFC = góc HDC = 90o.
Suy ra góc HFC + góc HDC = 180o
Suy ra HFCD là tứ giác nội tiếp
\(\Rightarrow\) góc HDC = góc HCD.
b) Vì M là trung điểm cạnh huyền của hình tam giác vuông ADH nên MD = MA = MH. Tương tự ta có ME = MA = MH
Suy ra MD = ME
Mà OD = OE nên \(\Delta\) OEM = \(\Delta\) ODM \(\Rightarrow\) góc MOE = góc MOD = \(\frac{1}{2}\) góc EOD
Theo qua hệ giữa góc nội tiếp và góc ở tâm cùng chắn cung, ta có góc ECD = \(\frac{1}{2}\) góc EOD
Theo ý a) ta có góc HFD = góc HCD = góc ECD
\(\Rightarrow\) góc MOD = góc HFD hay góc MOD = góc MFD
Suy ra tứ giác MFOD là tứ giác nội tiếp
\(\Rightarrow\) góc MDO = 180o - góc MPO = 90o \(\Rightarrow\) MD \(\perp\) DO
Chứng minh tương tự ta có MEFO là tứ giác nội tiếp
Suy ra 5 điểm M, E, F, O, D cùng thộc 1 đường tròn.

Hình gửi kèm

Do H là tâm của hình vuông ABCD nên:
A M → + B M → + C M → + D M → = A H → + H M → + B H → + H M → + C H → + H M → + D H → + H M → = 4 H M →
Do đó để A M → + B M → + C M → + D M → = H M →
⇔ 4 H M → = H M → ⇔ H M → = 0 → ⇔ H ≡ M
Đáp án D