Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chi tiết \(BM=DN=\dfrac{a}{3}\) hoàn toàn không cần thiết
a.
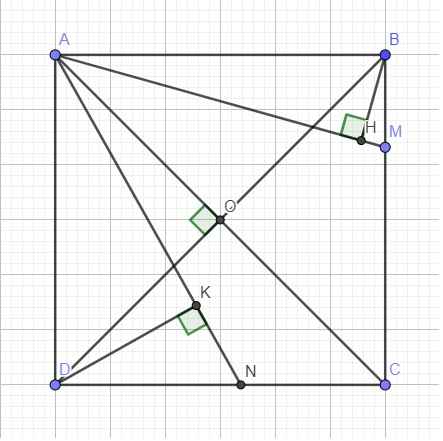
Ta có: \(AC\perp BD\) tại O (2 đường chéo hình vuông) \(\Rightarrow O\) thuộc đường tròn đường kính AB
\(AH\perp BH\) (gt) \(\Rightarrow\) H thuộc đường tròn đường kính AB
\(\Rightarrow\) 4 điểm A,B,O,H cùng thuộc đường tròn đường kính AB hay tứ giác ABHO nội tiếp
Hoàn toàn tương tự, 4 điểm ADKO cùng thuộc đường tròn đường kính AD nên tứ giác ADKO nội tiếp
b.
Trong tam giác vuông ABM vuông tại B với đường cao BH, áp dụng hệ thức lượng:
\(AB^2=AH.AM\)
Tương tự, trong tam giác vuông ADN:
\(AD^2=AK.AN\)
Mà \(AB=AD=a\Rightarrow AH.AM=AK.AN\Rightarrow\dfrac{AH}{AN}=\dfrac{AK}{AM}\) (đpcm)

A B C D M N H I
Kẽ NI // BC
\(\Rightarrow\frac{DN}{DC}=\frac{AI}{AB}=\frac{AM}{AH}\)
\(\Rightarrow\)MI // BH
\(\Rightarrow\widehat{IMB}=\widehat{MBH}\left(1\right)\)
Tứ giác IBCN có
\(\widehat{IBC}=\widehat{BIN}=\widehat{BCN}\)
\(\Rightarrow\)Tứ giác IBCN là hình chữ nhật
\(\Rightarrow\widehat{NBC}=\widehat{BCI}\left(2\right)\)
Xét tứ giác IMCB có
\(\widehat{IMC}=90\)(vì IM // BH và BH vuông góc AC)\
\(\widehat{IBC}=90\)
\(\Rightarrow\)Tứ giác IMCB là tứ giác nội tiếp đường tròn
\(\Rightarrow\widehat{IMB}=\widehat{ICB}\left(3\right)\)(cùng chắn cung IB)
Từ (1),(2),(3) \(\Rightarrow\widehat{MBH}=\widehat{NBC}\)
\(\Rightarrow\widehat{BMC}=90-\widehat{MBH}=90-\widehat{NBC}=\widehat{CNB}\)
\(\Rightarrow\)Tứ giác MBCN nội tiếp đường tròn
Hay M,B,C,N cùng nằm trên một đường tròn

a) \(\Delta NBM~\Delta DAM\left(g.g\right)\Rightarrow\frac{NM}{DM}=\frac{BM}{AM}=\frac{1}{2}\)
\(DM=\sqrt{AM^2+AD^2}=\sqrt{\frac{4}{9}a^2+a^2}=\frac{\sqrt{13}}{3}a\)
\(DN=\frac{3}{2}DM=\frac{\sqrt{13}a}{2}\)
\(NC=\sqrt{DN^2-DC^2}=\sqrt{\frac{13}{4}a^2-a^2}=\frac{3}{2}a\)
\(\frac{1}{EC^2}=\frac{1}{DC^2}+\frac{1}{NC^2}\Rightarrow EC=\frac{3\sqrt{13}}{13}a\)
b) \(\frac{1}{DM^2}+\frac{1}{DN^2}=\frac{1}{\frac{13}{9}a^2}+\frac{1}{\frac{13}{4}a^2}=\frac{4+9}{13a^2}=\frac{1}{a^2}\)