Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1( Hình mik đăng lên trước nha, mới lại phần bn nối điểm K với B, điểm F với D hộ mik nhé)
a) Xét tam giác EFA và tam giác CAB, có:
AE = AC ( giả thiết)
AF = AB (giả thiết)
Góc EAF = góc BAC (2 góc đối đỉnh)
=> ΔEAF = ΔCAB (c.g.c)
b) Vì ΔEFA = ΔCAB (Theo a)
=> Góc ABC = Góc EFA (cặp góc tương ứng)
=> EF = BC (cặp cạnh tương ứng) (1)
Mà EK = KF = 1/2 EF (2)
BD = DC = 1/2 BC (3)
Từ (1), (2) và (3)
=> KF = BD
Xét ΔKFB và ΔFBD, có
Cạnh BF chung
KF = BD (chứng minh trên)
Góc EFB = Góc ABC (chứng minh trên)
=> ΔKFB =ΔDBF (c.g.c)
=> KB = FD (cặp cạnh tương ứng)

Xét ΔABD và ΔEBD, ta có:
AB=BE ( gt)
Góc ABD= góc EBD ( Vì BD là tia phân giác của góc B)
BD chung
⇒ΔABD=ΔEBD(c-g-c)
b)Vì ΔABD=ΔEBD nên góc BAD= góc BED=90 độ( 2 cạnh tương ứng)
hay DE vuông góc với BC
c) Vì ΔABD=ΔEBD nên DA=DE ( 2 cạnh tương ứng)
Xét ΔADF và ΔEDC ta có:
góc FAD=góc CED(câu b)
AD=ED (cmt)
góc ADF=gócEDC( đối đỉnh)
⇒ΔADF=ΔEDC (g-c-g)
d,Xét ΔDAE và ΔDCF có:
DA=DC
Góc ADE=góc CDF (đối đỉnh)
DE=DF
⇒ΔDAE = ΔDCF (c-g-c)
⇒góc DAE=góc DCF (2 góc tương ứng)
MÀ 2 góc này ở vị trí SLT
⇒AE//CF
Đúg thì k
Mè sai cx k hộ nhen

A B D C E I
a) Ta có: tam giác ABD đều => AB = AD = BD; \(\widehat{ABD}=\widehat{ADB}=\widehat{BAD}\)
tam giác ABC vuông cân tại A
=> AB = AC; góc BAC = 90o
tam giác ADE vuông cân tại A => AD = AE; góc DAE = 90o
=> AC = AE
góc BAC = góc DAE
Lại có:\(\widehat{BAC}+\widehat{BAD}=\widehat{CAD}\)
\(\widehat{DAE}+\widehat{BAD}=\widehat{EAB}\)
\(\Rightarrow\widehat{CAD}=\widehat{EAB}\)
Xét \(\Delta ACD\)và \(\Delta AEB\)có:
AC = AE (cmt)
\(\widehat{CAD}=\widehat{EAB}\)(cmt)
AD = AB (cmt)
\(\Rightarrow\Delta ACD=\Delta ABE\left(c.g.c\right)\)

A B C D H E
a) Xét ΔABH vÀ ΔDBH có:
BH:cạnh chung
\(\widehat{AHB}=\widehat{DHB}=90^o\)
AH=DH(gt)
=> ΔABH=ΔDBH(c.g.c)
b)Xét ΔAHC và ΔDHC có:
AH=DH(gt)
\(\widehat{AHC}=\widehat{DHC}=90^o\)
HC: cạnh chung
=> ΔAHC=ΔDHC(c.g.c)
=> AC=CD
c) Xét ΔBHD và ΔEHA có:
\(\widehat{BHD}=\widehat{EHA}=90^o\)
DH=AH(gt)
\(\widehat{BDH}=\widehat{EAH}\) ( sole trong do AE//BD)
=> ΔBHD=ΔEHA(g.c.g)
=> BH=EH
=>H là trung điểm của BE

Ta có hình vẽ:
A B C D
a/ Ta có: \(\widehat{B}=\widehat{C}\) (GT) (1)
Ta có: \(\widehat{BAD}=\widehat{CAD}\) (GT) (2)
Mà tổng 3 góc trong tam giác = 1800 (3)
Từ (1),(2),(3) => \(\widehat{ADB}=\widehat{ADC}\) (*)
Ta có: \(\widehat{BAD}=\widehat{CAD}\) (GT) (**)
AD: cạnh chung (***)
Từ (*),(**),(***) => tam giác ABD = tam giác ACD (g.c.g)
b/ Ta có: tam giác ABD = tam giác ACD (câu a)
=> AB = AC (2 cạnh tương ứng)
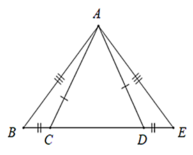

A B = A E B C = D E A C = A D ⇒ Δ A B C = Δ A E D c − c − c
Đáp án C