VH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
22 tháng 3 2019
Đáp án D
Với điểm M(1;-2;3). Gọi M 1 , M 2 , M 3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz thì tọa độ M 1 (1; 0; 0); M 2 (0 ;-2; 0) và M 3 ( 0; 0; 3).
Phương trình mặt phẳng M1M2M3 là:
x 1 + y - 2 + z 3 = 1
CM
29 tháng 1 2019
Chọn C.
Gọi 
Khi đó phương trình tiếp tuyến
M
0
là
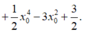
Ta có: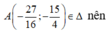 
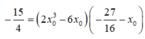
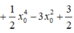
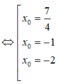
Không mất tính tổng quát của M 1 ( x 1 ; y 1 ) , M 2 ( x 2 ; y 2 ) , M 3 ( x 3 ; y 3 ) , ta có:
CM
21 tháng 3 2019
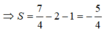
Đáp án B
vtpt của 0x
n
⇀
(1;0;0) vtcp của 0y
m
⇀
(0;1;0)
M 1 là hình chiếu của m lên 0x khi
M M 1 ⇀ . n ⇀ = 0 ⇔ m = 1 suy ra M 1 (1;0;0)
M 2 là hình chiếu của m lên0y khi M M 2 ⇀ . m ⇀ = 0 ⇔ n = 2 suy ra M 2 (0;2;0)
M 1 M 2 ⇀ (-1;2;0) là vtcp của đt M 1 M 2
CM
19 tháng 12 2017
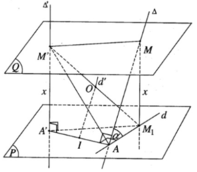
Vì mặt phẳng (P) qua A và vuông góc với Δ′ nên AA’ thuộc (P). Vì M thuộc ∆ mà d là hình chiếu vuông góc của ∆ trên (P) nên M 1 thuộc d. Vì MA ⊥ AA′ ⇒ M 1 A ⊥ AA′
Mặt khác M 1 A ⊥ M′A′ nên ta suy ra M 1 A ⊥ (AA′M′). Do đó M 1 A ⊥ M′A và điểm A thuộc mặt cầu đường kính M’ M 1
Ta có M′A′ ⊥ (P) nên M′A′ ⊥ A′ M 1 , ta suy ra điểm A’ cũng thuộc mặt cầu đường kính M’ M 1
Ta có (Q) // (P) nên ta suy ra
M M 1 ⊥ (Q) mà MM’ thuộc (Q), do đó M 1 M ⊥ MM′
Như vậy 5 điểm A, A’, M, M’, M 1 cùng thuộc mặt cầu (S) có đường kính M’ M 1 . Tâm O của mặt cầu (S) là trung điểm của đoạn M’ M 1
Ta có M ' M 1 2 = M ' A ' 2 + A ' M 1 2 = M ' A ' 2 + A ' A 2 + AM 1 2 = x 2 + a 2 + x 2 cot 2 α vì M M 1 = x
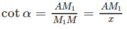
Bán kính r của mặt cầu (S) bằng (M′ M 1 )/2 nên
CM
19 tháng 4 2018
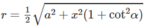
Chọn A
Ta có 
và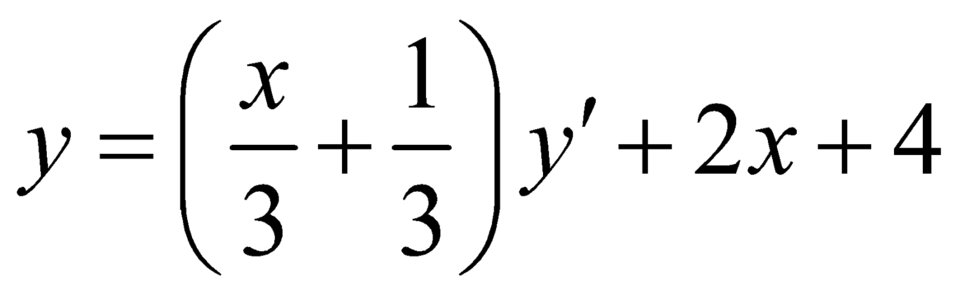 
,
Duy ra phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là 
, 
.
Đường tròn 
có tâm 
và bán kính 
.
Đường thẳng 
tiếp xúc với đường tròn 
khi và chỉ khi 
.
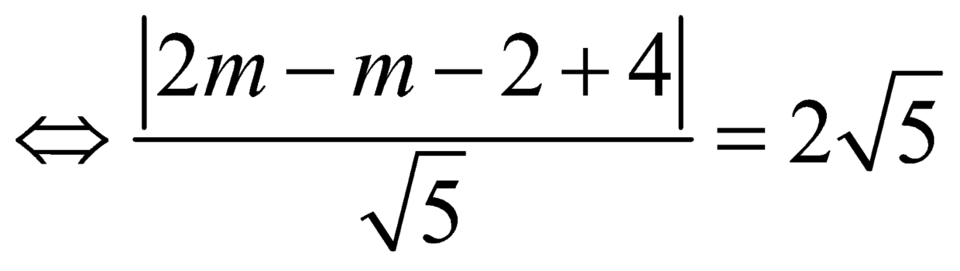
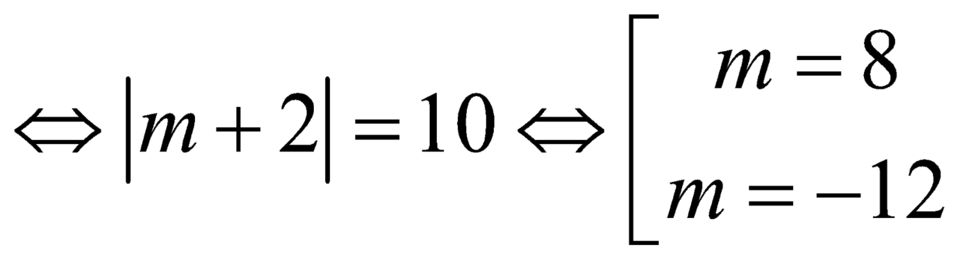Vậy 
.
CM
14 tháng 12 2017
Đáp án D
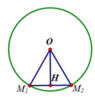
M 1 , M 2 thuộc đường tròn (T) có tâm O(0;0) và bán kính R=1
