
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


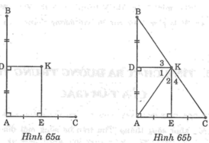
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.

a) Xét ΔOAHΔOAH và ΔOBHΔOBH ta có:
OA = OB (theo giả thiết)
HA = HB (H là trung điểm AB)
OH chung
⇒ΔOAH=ΔOBH(c−c−c)⇒ΔOAH=ΔOBH(c−c−c)
b) Ta có: ΔOAH=ΔOBHΔOAH=ΔOBH (chứng minh trên)
⇒∠AOH=∠BOH⇒∠AOH=∠BOH ( 2 góc tương ứng bằng nhau)
Hay ∠AOC=∠BOC∠AOC=∠BOC
Xét ΔOACΔOAC và ΔOBCΔOBC ta có:
OA = OB (theo giả thiết)
OC chung
∠AOC=∠BOC∠AOC=∠BOC
⇒ΔOAC=ΔOBC(c−g−c)⇒ΔOAC=ΔOBC(c−g−c)
⇒∠OAC=∠OBC⇒∠OAC=∠OBC(2 góc tương ứng)
Mà ∠OAC∠OAC= 900 nên ∠OBC∠OBC = 900
⇒CB⊥OB⇒CB⊥OB( điều phải chứng minh)
c) Ta có: ∠AOC=∠BOC∠AOC=∠BOC (chứng minh trên) (1)
Xét 2 tam giác vuông MIO và MIH ta có:
MI chung
IO = IH (Vì I là trung điểm của OH)
⇒ΔMIO=ΔMIH⇒ΔMIO=ΔMIH (Cạnh góc vuông – cạnh góc vuông)
⇒∠MOI=∠MHI⇒∠MOI=∠MHI (2 góc tương ứng)
Hay∠AOC=∠MHIHay∠AOC=∠MHI (2)
Từ (1) và (2) ta có: ∠BOC=∠MHI∠BOC=∠MHI (cặp góc ở vị trí so le trong)
⇒MH//OB⇒MH//OB (*)
Lại có:
HK⊥BCOB⊥BC}⇒HK//OBHK⊥BCOB⊥BC}⇒HK//OB (Quan hệ giữa tính vuông góc và tính song song của ba đường thẳng) (**)
Từ (*) và (**) ta có: MH và HK cùng thuộc một đường thẳng song song với OB.
Suy ra M, H, K thẳng hàng (điều phải chứng minh)
x O y A B H C
a) Xét tam giác AHO và tam giác BHO
có OH chung
HA=HB (GT)
OA=OB (GT)
suy ra tam giác AHO = tam giác BHO (c.c.c) (1)
b) Từ (1) suy ra góc AOC = góc BOC
Xét tam giác AOC và tam giác BOC có
OC chung
góc AOC = góc BOC
OA=OB (GT)
suy ra tam giác AOC = tam giác BOC (c.g.c)
suy ra góc OAC = góc OBC (hai góc tương ứng)
mà góc OAC =900
suy ra góc OBC = 900
suy ra CB vuông góc với OB tại B

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

a, xét hai tam giác ABM và ACM có AB=AC, MB=MC, AM chung \(\Rightarrow\) ABM=ACM (c.c.c)
b, AB=AC nên ABC là tam giác cân, M là trung điểm BC nên AM vuông góc với BC
c,xét 2 tam giác AEH và CEM có EA=EC, EM=EH, góc MEC= góc HEA nên hai tam giác đó bằng nhau (c.g.c)
d, theo câu c đã có tam giác AEH=CEM nên góc AHE= góc CME. Hai góc này ở vị trí so le nên AH // BC (1)
tiếp tục xét 2 tam giác DKA và DMB, có góc KDA=DBM, DK = DM. Mặt khác ta thấy DMEA là hinhf bình hành nên ME=AD=DB ( do ME cũng là đường trung bình của ABC)
nên suy ra tam giác DKA=DMB suy ra góc AKD=BMD, hai góc này ở vị trí so le nên AK// BC(2)
Từ 1 và 2 suy ra AH và AK cùng nằm trên 1 đường thẳng hay K,H,A thẳng hàng...
hình vẽ nào?
Hình vẽ?